3-13-1: キルヒホッフの法則
この単元の説明を読めば、キルヒホッフ則の符号ミスはもうしなくなるでしょう!
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント
・ キルヒホッフの第2法則 閉回路を1周したときの電圧降下=起電力
・ キルヒホッフの第1法則 導線のつなぎ目に入る電流の和=つなぎ目から出る電流の和
「電流保存則」
図1のような電気回路を考えてみよう。[ 電荷\(Q_1,Q_2>0\) とする。容量\(2C\) のコンデンサーの右極板を前もって正に帯電させておき、その後図1のように電池をつなげば、このような電荷分布は可能である。] 「回路」とは、1周した後で元の場所に戻るという意味合いの言葉。点線に沿って右回りに1周してみる。
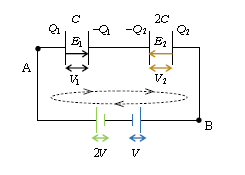
点Aからスタートして、点Bを経て、再び点Aに戻るときの電位の上がり下がりの様子を示したのが図2。図1で右向きにコンデンサーをたどるのが図2(a)、図1で左向きに電池をたどるのが図2(b)。各々の導線はひとつながりの導体を成すので等電位だ(電位の上がり下がりはない。3-06-1)。
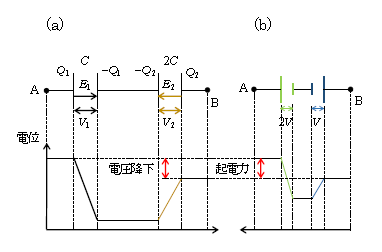
まずコンデンサーの電位を図2(a)の右向きにたどって調べよう。\(C\)については\(Q_1\)から\(-Q_1\) へ電場\(E_1\)があり、電場の向きに電位は下がるから、電位差\(V_1\)だけ電位が下がる。\(2C\)では\(-Q_2\)から\(Q_2\)へと電場\(E_2\)に逆行しており、\(V_2\)だけむしろ電位は上がる。なお、図1点線のような電位をたどる向きを回路の正の向きという。
次に電池を図2(b)の左向きにたどる。3-09-2でやった通り、電池は負極から正極へ電位を汲み上げるポンプの役目をしているから、緑の電池は\(2V\)だけ電位が上がるが、青の電池は\(V\)だけむしろ電位が下がる。
図2でコンデンサーでの電位の下がり分の合計を「電圧降下」(の合計)という。電池での電位の上がり分の合計を「起電力」(の合計)という。AからスタートしてAに戻るのが回路だから、当然
一周したときの下がり分の合計=上がり分の合計 となっている。つまり
電圧降下 = 起電力 これをキルヒホッフの第2法則という。 (1)
電圧降下を具体的に数式で表すと、 \(V_1-V_2\) (*)
となる。すなわち電位の上がり分\(V_2\)は負の電圧降下として扱う(例えば、5上がると言うのを\(-\)5下がると言っても同じという意味)。3-08-1でやった通り\(Q_1=CV_1,Q_2=2CV_2\)だから、
電圧降下(*)\(\displaystyle =\frac{Q_1}{C}-\frac{Q_2}{2C} \) とも書ける。 (2)
次に、起電力は数式で \(2V-V\) (3)
すなわち電位の下がり分\(V\)は負の起電力として扱う。
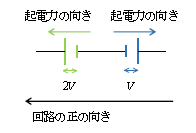
起電力は次のようにも扱える。まず、電池の正極から電流を押し流す向きを起電力の向きという(図3)。起電力の向きが回路の正の向きと一致しているときは正の起電力、逆向きのときは負の起電力として扱う。したがって図3の起電力は\(2V-V\)。
(2)(3)を(1)に代入して \(\displaystyle \frac{Q_1}{C}-\frac{Q_2}{2C}=2V-V \) (4)
これが第2法則の具体的な数式だ。
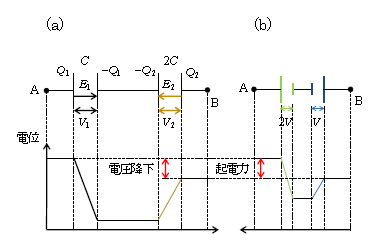
ところで、回路の正の向き(電位をたどる向き)を図1の左回り(図2(a)の左向き、(b)の右向き)と逆転してみよう(図2を右下に再掲した)。
この場合、電位は\(V_2\)下がって\(V_1\)上がるから、
電圧降下\(\displaystyle =\frac{Q_2}{2C}-\frac{Q_1}{C} \) (2′)
(2′)は(2)の逆符号の式である。また、図2(b)の右向きを回路の正の向きとしているから、
起電力\(=V-2V\) (3′)
(3′)は(3)の逆符号の式である。(2′)(3′)を(1)に代入すると、(4)と同じ式が得られる。つまり、回路の正の向きを逆にすると、電圧降下も起電力も同時に逆符号になるから、(1)式 電圧降下=起電力 の第2法則は変わらない。結局、回路の正の向きは右回り・左回りどちらにとってもよい。
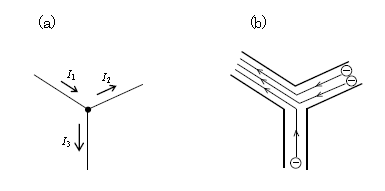
最後の話に移ろう ―― 図4(a)の黒丸は導線のつなぎ目(結節点ともいう)で、
つなぎ目に入る電流の和=つなぎ目から出る電流の和 (5) をキルヒホッフの第1法則という。
数式では \(I_1=I_2+I_3\)
第1法則の成り立つ理由を説明したのが、つなぎ目をモデル化して拡大した図4(b)で、微小時間\(\Delta t \)の間のスナップショットだ。3-06-1でやった通り、自由電子⊝の流れる向きと逆向きが電流の向き。例えば、電子がつなぎ目に右斜め上から2個入り、下から1個入り、つなぎ目から左斜め上に3個出ていく様子が描かれている。電子は「通常」途中でこの自然界から消えたり新たに生まれたりしない(「通常」と断った理由については最後に述べる)。また、\(\Delta t \)の間に金属正イオンがはぎ取られたり新たに付着することも、実験的には想定していない。すると、
つなぎ目から出る電子数=つなぎ目に入る電子数 これから直接(5)が結論される。
結局キルヒホッフの法則の第1法則は、つなぎ目に入る直前・直後での単位時間あたりの電荷保存則、すなわち電流保存則であると言える。
[ 「通常」と断ったのは ―― 実は素粒子(宇宙の最小構成要素の粒子)レベルで言うと、例えば陽電子という素粒子が導線の外から入ってきて、導線内の電子という素粒子と対消滅なる反応をし、陽電子・電子ともに消えて代わりに光子という素粒子が複数個生じるといった現象が可能である。この場合電子はこの自然界から消えている。が、電気回路の分野では「通常」そういった現象を想定していないし、そもそも陽電子・電子の電気量の大きさは1.6×10\(^{-19}\)C(光子は電気量0)なので、そういった現象で回路を流れるmA程度の電流に影響が出ることはない。 ]


