3-11-1: 誘電体
誘電体についての重要事項を明快に解説します！
※ ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント
・ 誘電体中の電場\(E’\)は真空中の電場\(E\)よりも弱まりはするが、０とならずに残る
比誘電率を\(\epsilon_r\)として \(\displaystyle E’=\frac{1}{\epsilon_r} E\)
誘電体の誘電率
\(\epsilon=\epsilon_r\)×真空の誘電率\(\epsilon_0\)
電気をよく通す物質を導体というのに対し、電気をほとんど通さない物質は不導体・絶縁体などといい、特にコンデンサーの分野では誘電体という。誘電体は不導体だ。誘電体には炭素を含むものが多いので、炭素を例にとって説明しよう。
炭素原子は負電荷の電子6個と原子核（正電荷の陽子6個を含む）から成り、電気的に中性。電場をかけていない状態では負電荷の分布の中心と正電荷の分布の中心が一致している。この炭素原子を図１(a)のように球形で図示しておく。一方、炭素原子が電場中に置かれると（図１(b)）、正電荷は電場の向き(下向き)に電気力を受けて分布の中心が下がり、負電荷は電場と逆向きに電気力を受けて分布の中心が上がる。これを原子の「分極」（＋とーが分かれたという意味合いの言葉）という。この炭素原子を(b)のように楕円体に＋、ーを付けて表しておく。ここは正確に球形や楕円体になっているという意味ではなく、「遠目からみると大体こんな感じ」ぐらいの受け止めをしてほしい。[ そもそも原子の大きさ程度のものを正確に議論するには、大学の量子力学を用いなければならず、原子の形状を語るにはいろいろな問題がはらんでいるということだけコメントし、これ以上は深入りしない。 ]
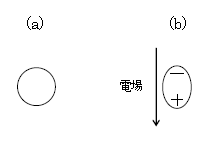
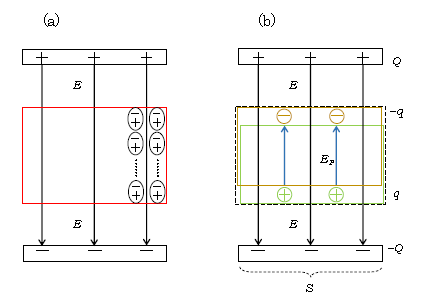
図２(a)は直方体の誘電体(赤色)をコンデンサーの電場\(E\)中に置いたときのふるまい。導体を電場中に置いたときに起こる現象を「静電誘導」と言ったのに対し、誘電体を電場中に置いたときに起こる現象は「誘電分極」と言う。(a)には楕円体の炭素原子が6個だけ書かれている。しかし、実は炭素原子はざっと10\(^{20}\)個あり、各々は(a)のように整然と配列してはいず、乱雑に運動をしている。また、誘電体の中には炭素だけでなく、酸素や水素などもあったりする。現実は熾烈を極めて複雑なのだ。そこで、10\(^{20}\)個もの膨大な数に上る対象の統計的平均のふるまいを捉えることにしよう。高校物理としては、次のような大胆な簡単化をすれば十分 ―― 図2(b)のように、誘電体を電子だけが一様にぎっしり詰まった箱(黄色)と、原子核だけが一様に詰まった箱(緑色)から成ると捉える。電気的に中性の誘電体を考えるなら、負電荷の合計と正電荷の合計は等しい。電子の箱は電場と逆向きに力を受けて少し上がり、原子核の箱は電場の向きに力を受けて少し下がる。2つの箱が重なり合ったところでは＋ーが等量あって電荷分布は現れないが、電子の箱が原子核の箱に対して少し上に出っ張った部分では⊖が現れる。原子核の箱が電子の箱に対して下に出っ張った部分では⊕が現れる。誘電体の電荷は上・下表面にだけ分布し、この⊕⊖を「分極電荷」という。
ここで誘電体（図2(b)の点線枠内）をいったん真空に見立てて、コンデンサーが点線枠内の真空中につくる電場\(E\)(下向き)を求めたとする。次に分極電荷が点線枠内の真空中につくる電場\(E_P\)(上向き。電気力線は⊕から出て⊖に入る。なお、Pは分極polarizationを表す添え字）を求めたとする。すると、それらを合成した電場\(E’\)が誘電体中の電場となる。 (1)
さて、図3(a)には導体をコンデンサーの電場\(E\)中に置いたときのふるまい（3-06-1の静電誘導）が示してある。導体中の自由電子はその名の通り「自由に」流れて⊝と⊕が分布し、⊕から⊝に生じる電場がコンデンサーの電場を導体内で完全に打消して、導体内部の電場は０になるのだった。これに比して誘電体は不導体であるから、「自由に」動き回れる電荷を持たない。図2(b)で\(E_P\)は\(E\)を弱める方向に生じるものの、打消しは不完全（\(E_P<E\)）となる。結果として、誘電体内部の合成電場\(E’\)は、コンデンサーの電場(真空中の電場)\(E\)よりも弱まるが、０とならずに残る（図3(b)）。この図は⊖から⊕に電気力線が生じるという意味ではもちろんなく、図2(b)のように下向きの\(E\)が上向きの\(E_P\)で弱められて、合成電場\(E’\)が下向きに残ったという意味である。
ここで、\(E’\)が例えば\(E\)の\(\frac{1}{3}\)に弱められるなら、比誘電率\(\epsilon_r\)\(=3\)（イプシロンアールと読む）（rはrelative相対的なという意味の添え字）であると言う。すなわち比誘電率とは真空中の電場の弱め方の度合いである：
誘電体中の電場\(\displaystyle E’=\frac{1}{\epsilon_r} \)×真空中の電場\(E\) (2)
\(\displaystyle\)(2)式を比誘電率の定義式としよう。[ 大学の電磁気学では比誘電率を異なる流儀で定義するが、高校物理としては(2)を定義式 ―― 誘電体分野の出発点の式にすると使い勝手がよい。 ] また、
誘電体の誘電率\(\epsilon=\)比誘電率\(\epsilon_r\)×真空の誘電率\(\epsilon_0\) (3)
と定義する。(2)より比誘電率\(\epsilon_r\)は単位を持たない量で、\(E’\)は\(E\)より弱まるから\(\epsilon_r>1\)。すると(3)より誘電率\(\epsilon\)は真空の誘電率\(\epsilon_0\)と同じ単位を持つ量であることが分かり、\(\epsilon_r>1\)だから\(\epsilon>\epsilon_0\)である。
ここで練習題として、図2(b)(右に再掲)を見ながら分極電荷\(q\)(>0)がコンデンサーの電荷\(Q\)(>0)の何倍になるかを求めてみよう。(2)を誘電体分野の出発点の式とするのだが、そもそも\(\displaystyle \frac{1}{\epsilon_r} \)に弱まった理由は(1)の段落(右に再掲)に述べた内容で、それを数式に表すと
\(E-E_P=E’ \) (4)
\(E’ \)には(2)を代入、また3-08-1より\(\displaystyle E=\frac{Q}{\epsilon_0 S} \) 及び \(\displaystyle E_P=\frac{q}{\epsilon_0 S} \)を代入できる。すると(4)は
\(\displaystyle \frac{Q}{\epsilon_0 S}-\frac{q}{\epsilon_0 S}=\frac{1}{\epsilon_r} \frac{Q}{\epsilon_0 S} \) 分母の\(\epsilon_0 S\)を払って
\(\displaystyle Q-q=\frac{1}{\epsilon_r} Q\) よって \(\displaystyle q=\left(1-\frac{1}{\epsilon_r}\right) \:× Q\) と求まる。
[ なお、\(\displaystyle q=Q-\frac{1}{\epsilon_r}Q<Q \) すなわち\(q<Q\)である ]
\(\epsilon_0\)の単位は3-05-1で[C\(^2\)/(N\(\cdot\)m\(^2\))]であると述べた。一方、3-08-1の容量\(\displaystyle C=\frac{\epsilon_0S}{d} \)の式を用いると、
\(\displaystyle\)\(\epsilon_0\)の単位\(=\)\(C\)の単位×\(d\)の単位÷\(S\)の単位\(=\)[F×ｍ÷ｍ\(^2\)]\(=\)[F/ｍ]
とも表せる。[F/ｍ]の方が簡単で覚えやすい。