3-12-1: コンデンサーへの誘電体の全挿入

この単元はコンデンサーの3大公式の格好の練習題にもなっています！　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

※　ページ最上部の（一部スマホでは右上または下側の $\equiv$ 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

　図1はコンデンサーの極板間を誘電体(赤色)ですき間なく満たした状況。3-08-1のコンデンサーの3大公式に基づいて、ポイント(1)(2)を示そう。

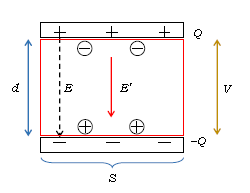
　第1公式：電荷から電場ができる。真空中の電場$\displaystyle E=\frac{Q}{\epsilon_0 S}$
　　誘電体中の電場は3-11-1の通り $\displaystyle E’=\frac{1}{\epsilon_r} E$ だから、$\displaystyle E’=\frac{1}{\epsilon_r}\frac{Q}{\epsilon_0 S}$
　第2公式：電場に沿って電位が下がる。電位差$\displaystyle V=E’d=\frac{1}{\epsilon_r}\frac{Q}{\epsilon_0 S} d=\frac{1}{\epsilon_r}\frac{d}{\epsilon_0 S} Q$
　第3公式 : $Q$は$V$に比例。$Q=C’V$と書ける。
　よって $\displaystyle C’=\frac{Q}{V}=\frac{\epsilon_r\epsilon_0 S}{d}$
　$\displaystyle C=\frac{\epsilon_0 S}{d}$ だから $C’=\epsilon_r C$　これがポイント(1)である。
　3-11-1の通り $\epsilon_r\epsilon_0=\epsilon$ だから $\displaystyle C’=\frac{\epsilon S}{d}$　これがポイント(2)である。
　真空中のコンデンサーの容量が$\displaystyle C=\frac{\epsilon_0 S}{d}$ であるのに対して、誘電体を極板間にすき間なく満たしたときの容量が$\displaystyle C’=\frac{\epsilon S}{d}$ 。これが真空の誘電率$\epsilon_0$、誘電体の誘電率$\epsilon$というネーミングのそもそもの意味合いである（3-05-1の問題提起に対する答）。

　ちなみに、誘電体はなぜ役に立つのかと言うと、大きく2つの理由がある。
　第1は容量が$\epsilon_r$倍に増えること。コンデンサーは電荷をたくわえる装置で、$Q=CV$だから容量$C$が大きいほど$Q$が大きく、電荷をたくわえる装置としての有用性が増す。
　第2は、本来極板どうしは極板間引力で引き合っているので、放っておくと正極板と負極板が接触して「中和」してしまう。ところが電気を通さない誘電体を正・負極板の間に挟めば中和の心配はない。
　市販のコンデンサーは、その種類も大きさも実に多種多様であるが、ほんの一つだけ例を挙げると ―― 2枚のアルミ箔を極板として、フィルム上の誘電体をアルミ箔・誘電体・アルミ箔・誘電体の順序で重ね、例えば幅1cm程度の「のり巻き状」に巻いたコンデンサーがある。こうすると、幅1cm程度でも極板面積$S$がかなり広く取れ、しかも極板間隔$d$がかなり狭くなり、容量$\displaystyle C’=\frac{\epsilon S}{d}$がかなり大きく取れる。