2-11-1: 弦の固有振動

重ね合わせの原理で生じる現象の最後 ―― 両端に節・腹の条件の付いた定常波「固有振動」　→　＜例題＞は2-11-2へ　　　　　　　　

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

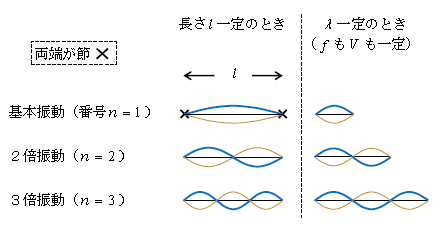
　弦に波を起こすときには、しばしば弦の両端が固定される。生じた波は左端でも右端でも反射されるから、2-07-1の入射波と反射波が重なり合って「形の等しい２つの波が\(＋V,-V\)」の状況、つまり定常波が生じる。ただし両端は固定された固定端だから、両端ともに節。すると図１のような波形は許されても、図２のように右端が腹となる波形は許されない（なお、青線から黄色の線は最短で\(\frac{1}{2} \)周期経っている）。

　定常波というジャンルの内、限られた波形だけが許される場合を特に固有振動という。ここでは弦の固有振動を扱う。次の2-12-1では気柱の固有振動を扱う。なお、弦の固有振動は空気中に音波を生じさせる。弦は弦楽器の原型だ。

　さて、固有振動では波の基本量\(V,\lambda, f\)を押さえることが大切。
　まず、弦を伝わる波の速さ\(\displaystyle V=\sqrt{\frac{S}{\rho} } \)の公式は覚えておこう（その証明は当面は不要）。\(S\)は弦の張力、\(\rho \)は弦の線密度。ふつう密度と言えば1m\(^3\)あたり何\(\text{kg} \)という単位体積あたりの質量を指すが、「線」密度とは単位長さあたりの質量、つまり1mあたり何\(\text{kg} \)という量で、ゆえに単位は[\(\text{kg/m} \)]。
　次に\(\lambda, f\)であるが、
1⃣　初めに、弦の長さ\(l\)が一定の場合を考える。
　波長\(\lambda \)とは、サインカーブ１個を波１個と数えたときの「波１個分の長さ」のことだから、弦の中に含まれる波の数さえ分かれば、\(\lambda\)=波１個分の長さ=\(\displaystyle \frac{l}{波の数} \)と求まり、後は\(\displaystyle f=\frac{V}{\lambda } \)とすれば\(f\)も求まる。
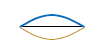
　図３の形を「腹１個」と呼ぼう。これは\(\frac{1}{2} \)波長分だから、波の数\(\frac{1}{2} \)に相当。

　この腹の数1,2,3,\(\cdots \)に対応して\(n\)=1,2,3, \(\cdots \)と番号を付け、それぞれ基本振動、２倍振動、３倍振動、･･･ と呼ぶ（図４）。
　すると、\(n\)倍振動 ―― 腹\(n\)個 ―― 波の数\(\displaystyle \frac{1}{2} ×n \)　
―― \(\displaystyle \lambda =\frac{l}{波の数} \) \(\displaystyle=\frac{l}{\frac{1}{2} ×n} = \frac{2l}{n} \)、　\(\displaystyle f＝\frac{V}{\lambda} =\frac{n}{2l} \sqrt{\frac{S}{\rho} } \)     　(＊)

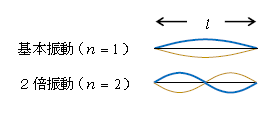
　この\(\lambda ,f \)の公式は覚える必要はない。波の数が\(\frac{1}{2} ×n \)であることさえ理解できていれば、(＊)の考え方によりあっという間に求まるから。

2⃣　次に、\(\lambda \)が一定の場合を考えよう。
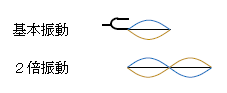
　\(\lambda \)一定の状況が生じるのは、例えば一定の振動数\(f\)のおんさの金属部分に弦の端をつなぐ場合だ（図５）。金属部分が1sあたり\(f\)回振動すると、それにつながれた弦も1sあたり\(f\)回振動するから、弦の振動数はおんさと同じ\(f\)に一定に保たれる。さらに弦の張力\(S\)、線密度\(\rho \)を一定に保てば、波の速さ\( V=\sqrt{\frac{S}{\rho} } \)も一定。ゆえに\(\lambda =\frac{V}{f} \)も一定となる、そういう状況。\( \lambda \)一定だから、弦の長さ\(l\)を大きくしていくと（図５の上から下に行くと）、順に基本振動、２倍振動、３倍振動、･･･ が現れる。この場合も(＊)の考え方は成り立つ。

3⃣　最後に、\(l,\lambda ,f,V \)様々なものを実験ごとに変えていく場合がある。このときも、やはり(＊)の考え方は成り立つ。(＊)は万能だ。