2-12-1: 気柱の固有振動
弦に続いて、気柱の固有振動をしっかり理解しましょう! → <例題>は2-12-2へ
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント
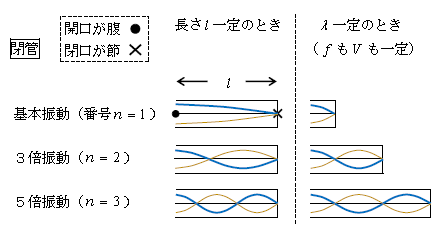
・ 気柱は開口が腹、閉口が節
・ 常温付近の温度\(t\)[℃]で音速\(V\)[m/s]\(=331.5+0.6t\)
・ 閉管は番号\(n\)のときの波の数は\(\displaystyle \frac{1}{4} ×(2n-1) \)
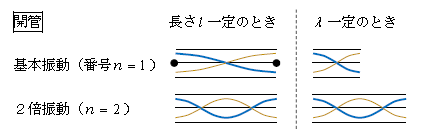
・ 開管は番号\(n\)のときの波の数は\(\displaystyle \frac{1}{4} ×2n \)
気柱とは例えばガラス管だ。両開きのものを開管、片開き・片閉じのものを閉管という。両方とも重要だが、閉管を中心に説明していこう。
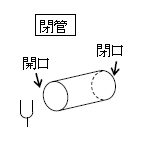
閉管の開口側から例えばおんさで音を送り込むと、閉口で反射され、また開口に壁はないが媒質(空気)の状況が変わる境目として開口でも反射が起こる。すると「形の等しい2つの波が\(+V,-V\)」で重なって定常波が立つ。音波は縦波だから、媒質粒子の振動は波の伝わる方向に平行、つまり管に沿った方向。閉口にぶつかると粒子はこの方向に振動できないから閉口は節、開口では振動できるから開口は腹となる。よってポイントの図のような固有振動が生じる。気柱の固有振動は開口から空気中へと音波を生じさせる。気柱は管楽器の原型である。
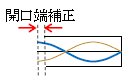
参考 なお現実には腹の位置が開口より少し外に出る扱いをする(理由は入試の範囲外)。この外に出る距離のことを開口端補正という。以下では開口端補正はないものとする。
固有振動は2-11-1と同様に波の基本量\(V,\lambda ,f \)を押さえよう。
\(V\)は音速で、ポイントの通りの公式が成り立つ(成り立つ理由は当面は知らなくてよい)。この式から、温度\(t\)が高くなるほど音速\(V\)は速くなると分かる。例えば\(t\)=15℃を代入すると、\(V\)≒340m/s。
\(\lambda ,f \)については、
1⃣ 管の長さ\(l\)一定の場合 2⃣ \(\lambda \)一定の場合 3⃣ \(l, \lambda, f, V \)様々なものを変えていく場合 ―― 全て同じ考え方ができる。つまり管の中に含まれる波の数を求めればよい。
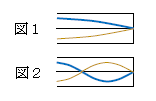
そのために、図1の波形に注目する。これは\(\frac{1}{4} \)波長分だから、波の数\(\frac{1}{4} \)に相当。すると図2は波の数\(\frac{3}{4} \)。結局、波の数は\(\frac{1}{4} ,\frac{3}{4} ,\frac{5}{4} ,\cdots \)と数えられる。波の数は\(\displaystyle \frac{1}{4} ×(2n-1) \)。
よって \(\displaystyle \lambda =\frac{l} {波の数} = \frac{l} {\frac{1}{4} ×(2n-1) } =\frac{4l} {2n-1} \)
\(\displaystyle f=\frac{V}{\lambda}=\frac{(2n-1)}{4l}\)
なお、波の数の比が\(\frac{1}{4} :\frac{3}{4} :\frac{5}{4} : \cdots \)=1:3:5:\(\cdots \)だから、名前は基本振動、3倍振動、5倍振動、・・・ と付いている。また、弦では\(n\)は腹の数だったが、気柱では閉管・開管ともに\(n\)は節の数である。
音を送り込むおんさによって固有振動が生じたならば、おんさによって気柱が共鳴したという。このとき気柱から音が強く聞こえてくる。送り込んだ音はそのまま気柱内に伝わるから、送り込んだ音の振動数と気柱に生じた固有振動の振動数は等しい。


