1-45-1: ばねの両端 ー 重心から見た相対運動 ＃その1 ＜動画あり＞

ばね相互作用の直観的な説明を明快にします！　→　＜続き＞は1-45-2,1-45-3,1-45-4へ ; michisanpo – YouTubeで関連動画を見るのも役に立ちます。よければチャンネル登録お願いします。　
https://www.youtube.com/watch?v=nphtjtJlTZ8　　　　　　

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

　この単元のタイトル「重心から見る」とは、重心速度\(v_G\)で動く観測者(以後単に人と呼ぶ)から見るということ。ところでタクシーに乗っている人から見ると自分の足元は止まって見えるのと同様に、\(v_G\)で動く人から見ると足元の重心は止まって見える。つまり、重心を固定した上で、2物体が相対的にどのような運動をするかを考えていくことにしたい。この単元では運動方程式を立てることなく、直観的にばね相互作用の時間変化を調べる（「時間変化を調べる」とは時刻tの位置x,速度vを求めること）。実は運動方程式は既に1-44-1で立てた。運動方程式を用いた数学的な考察は1-45-3でやる。
　問題設定は1-44-1と全く同じ ―― 自然長\(l\)でばね定数\(k\)の軽いばね、質量がそれぞれ\(m_1,m_2\)の球1,2、なめらかなで水平な床に沿って右向きを正とする\(x\)軸、任意の時刻\(t\)での球1,2それぞれの（床から見た）\(x\)座標を\(x_1,x_2\)、速度を\(v_1,v_2\)、加速度を\(a_1,a_2\)とし、力としては弾性力\(f\)のみを考える。 ―― さらに、初期値は印＊を付けて初期位置\(x^*_1,x^*_2\)、初速度\(v^*_1,v^*_2\) のように表す。また、重心から見た相対的な量は、大文字を用いて相対位置\(X_1,X_2\)、相対速度\(V_1,V_2\)、相対初期位置\(X^*_1,X^*_2\)、相対初速度\(V^*_1,V^*_2\)と表す。
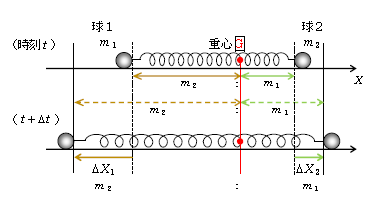
　重心Gは、1-43-1の通り\(x_1,x_2\)を質量の逆比\(m_2:m_1\)に内分する点。ゆえに、重心Gを固定して相対座標の原点Oに取れば、任意の時刻\(t\)での重心から見た相対位置も\(X_1:X_2=m_2:m_1\)のように質量の逆比になることは必然である（図１）。ということは、任意の時間間隔\(\Delta t\)での相対変位は、球1,2どうし互いに逆向きで、\(|\Delta X_1|:|\Delta X_2|=m_2:m_1\)。とくに\(\Delta t→0\)にすれば
　\(\displaystyle \left|\lim_{\Delta t → 0} \frac{\Delta X_1}{\Delta t}\right|:\left|\lim_{\Delta t → 0}\frac{\Delta X_2}{\Delta t}\right|=m_2:m_1\)　　∴　\(|V_1|:|V_2|=m_2:m_1\)　
　以上をまとめると、重心から見ると、2球の
　変位は互いに逆向きで|変位|は質量の逆比；速度も互いに逆向きで|速度|は質量の逆比　となる。　(☆)

　では、話を具体的にするために
　\(m_1=m,m_2=2m\) ; \(x^*_1=0,x^*_2=l\)（\(t=0\)で自然長の状態）; \(v^*_1=v>0,v^*_2=0\) 　　(1)
としよう。
　まず、1-44-1の通りばね相互作用では重心は(床から見て)等速だから、重心速度\(v_G\)(1-43-1)は初期値のまま一定、すなわち
　\(\displaystyle v_G=\frac{m_1v_1+m_2v_2}{m_1+m_2}=\frac{mv+2m0}{m+2m}=\frac{v}{3}\)　　[ (1)を代入した ]
　次に、重心から見た球1,2の相対初速度\(V^*_1,V^*_2\)は、「重心から見た」を引き算する公式(1-30-1)より
　\(\displaystyle V^*_1=v^*_1-v_G=v-\frac{v}{3}=\frac{2v}{3}\)
　\(\displaystyle V^*_2=v^*_2-v_G=0-\frac{v}{3}=-\frac{v}{3}\)
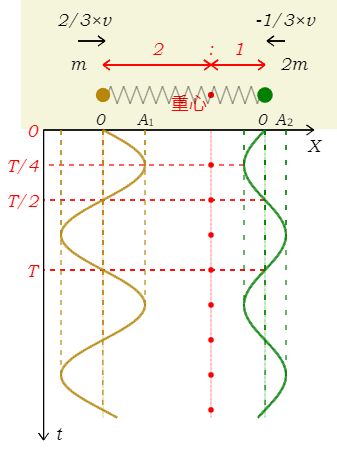
(☆)の通り、(相対)初速度も互いに逆向きで|初速度|は質量の逆比になっている。(1)より\(t=0\)では自然長の状態（弾性力の働かないつり合いの状態）だから、球１の時間変化は1-24-2: 単振動のx-tグラフの4パターン の「つり合い点で正の初速度を与える」場合に相当し、図２のような＋sin型のグラフになる（\(t\)軸を下向きに取った）。同様に、球2は「つり合い点で負の初速度を与える」場合だから、-sin型のグラフ。これがばね相互作用を重心から見た場合の典型的な運動である、すなわち、2球が互いに逆向きに動きつつ、同じ周期\(T\)で単振動する。振幅も質量の逆比(\(A_1:A_2=2:1\))。逆比であるがゆえに、軽い球の方が重い球より振幅が大きい。

　この重心から見た相対運動に、一定速度\(v_G\)の重心運動を組合わせると、床から見た運動は図３のようになる。

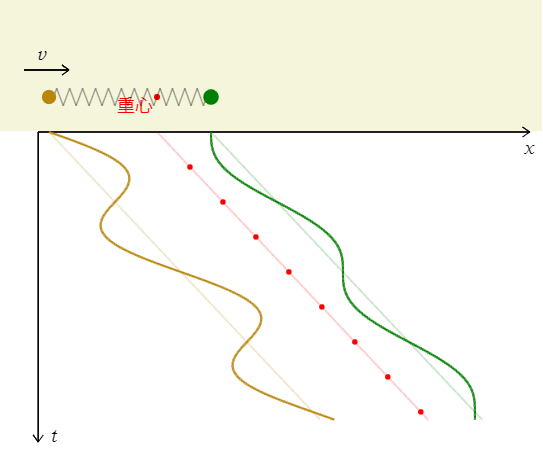
　これを見て一目瞭然なことは、床から見ると、球1,2は全体的には右へ右へと移動していくから、決して初期位置に戻ってこない。ということは、床から見た球1,2の運動は単振動ではない（単振動なら初期位置に何度も何度も戻ってくる）。単振動のような単純な運動とはならず、床から見ると、床から見た重心の等速度運動と重心から見た単振動の組合せになる。ばね相互作用を1-43-1:重心運動 とこの単元の重心から見た相対運動に分けて考えるそもそもの動機は、ここにあったのである。 [ michisanpo – YouTubeの関連動画も参考のこと　→　https://www.youtube.com/watch?v=nphtjtJlTZ8 ]　　　　　　
　さて、振幅\(A_1,A_2\)や周期\(T\)の計算であるが、それは次の単元1-45-2に回すことにする。