1-35-1: 慣性力

慣性力を正確に理解しておきましょう！　→　＜例題＞は1-35-2へ　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

　今まで一切触れてこなかったのであるが、運動方程式は、つねに大地上(あるいは床上)に静止している観測者の立場からものを見ながら立てていた。これを「静止座標系」から見て運動方程式を立てるという言い方をする。この単元では、加速度運動する観測者の視点に立ってものを見ることにしよう。すなわち「加速度座標系」から見て運動方程式を立てるとどのようになるかを扱う。
　図１で\(x\)-\(y\)とあるのが静止座標系(以後、静止系と略す)。これは大地に固定された座標系である。一方、\(x’\)-\(y’\)とあるのが観測者Pとともに加速度\(\vec{A}\)で動く加速度座標系(以後、加速系Pと呼ぶ)。物体の加速度\(\vec{a}\)と区別して、観測者Pの加速度は大文字の\(\vec{A}\)としてある（なお、\(\vec{A},\vec{a}\)の向きは適当に取った）。

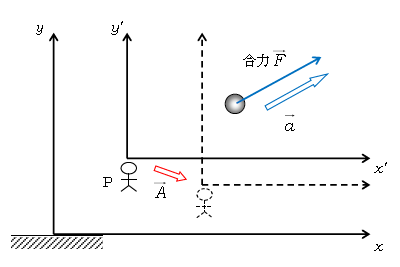
　まず、静止系から見た運動方程式は　\(m\vec{a}=\vec{F} \;\, \)　　　　 (1)
　(1)は1-05-1で述べた通り、宇宙の根本原理（我々の宇宙は運動方程式が成り立つようにできている）であるが、もっと正確には、我々の宇宙は運動方程式が「静止系から見て」成り立つようにできている。
　次に加速系Pから見ると、物体の加速度は相対加速度\(\vec{a’}=\vec{a}-\vec{A}\)で見えていることに注意しよう。1-30-2の通り、Pから見た相対加速度は「Pから見た」のPの加速度\(\vec{A}\)を引き算する。すると、運動方程式「力によって加速度が生じる」は \(m\vec{a’}=\vec{F}\)　すなわちPから見た運動方程式
　\(m\vec{a}-m\vec{A}=\vec{F} \, \)　？　　　　　　　　　　　　　　　　(2)
　もちろん宇宙の根本原理(1)の方が正しいので、このままでは(2)の方程式は正しくない。左辺で観測者Pの加速度\(\vec{A}×m\)の引き算をしている分(1)と食い違ってしまっている。そこで、右辺も\(m\vec{A}\)の引き算をしてみよう:
　　\(m\vec{a}-m\vec{A}=\vec{F}-m\vec{A} \,\)　　　　　　　　　　　　　 (3)
　(3)は(1)と同値なので正しい方程式となった。通常この左辺\(=m(\vec{a}-\vec{A})=m\vec{a’}\)と書いて、
　加速系Pから見た運動方程式　\(m\vec{a’}=\vec{F}+(-m\vec{A}) \)　　(4)　
となる。(1)と(4)の違いは２点。１つ目は左辺の加速度\(\vec{a}\)が相対加速度\(\vec{a’}\)に置き換わっていること。２つ目は右辺に新たな項\((-m\vec{A}) \)が加わっていること。この\((-m\vec{A}) \)を慣性力という。慣性力の向きは\((-\vec{A})\)の向き、すなわち観測者の加速度\(\vec{A}\)と逆向きである。慣性力の大きさは\(m|\vec{A}|\)である。
　通常の力\(\vec{F} \)だったら「何から」働く力かが言える（例えば摩擦力だったら「床面から」物体に働く）。が、慣性力は(4)を(1)と同値にするために数学的に\((-m\vec{A}) \)と書き加えた((3)を見よ)だけのもの、言わば数学的つじつま合わせの項にすぎないから、「何から」働く力ということが言えない。ということは作用反作用の法則を満たさない（慣性力\((-m\vec{A}) \)の反作用など存在しない）。こういったことから慣性力はみかけの力であるという言い方をする。
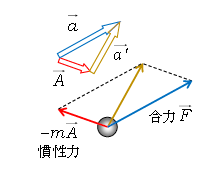
　図２には相対加速度\(\vec{a’}=\vec{a}-\vec{A}\)の作図が示してある。また、\(\vec{a}\)の向きには\(\vec{F}\)が書かれていて、さらに\(\vec{A}\)と逆向きに慣性力\((-m\vec{A})\)が書かれている。(4)の意味内容は、\(\vec{A}\)で加速度運動する観測者Ｐからすると、この\(\vec{F}\)と\((-m\vec{A})\)のベクトル和(黄色い矢印)の向きに、物体は相対加速度\(\vec{a’}\)を生じるように見えるということである。

　よく経験するように、加速度\(\vec{A}\)で急発進する電車の乗客は、元々真っ直ぐぶら下がっているつり革が、電車の進行方向と逆向きに傾くのを見る。これはまさに慣性力\((-m\vec{A})\)で\(\vec{A}\)と逆向きに傾いたのであるが、この際の慣性力という用語のニュアンスは ―― 急発進する前のつり革には力が働いていないから、慣性の法則(力が働かないと、物体は等速、特に初め静止していれば静止し続ける)によって、その場にとどまっていようとする。ということは、電車が急発進すると、電車の進行方向と逆向きにつり革を引き留めておこうとするような慣性の法則的な効果が生じる。それで慣性力という名が付いている
　Pが動いていても等速運動しているような場合、つまり観測者Pの加速度\(\vec{A}=\vec{0} \)であるような場合、慣性力\((-m\vec{A})=\)\(\vec{0} \)であることに注意しよう。例えば、電車が動いていても時速30kｍで等速運動している場合は、つり革は傾かない。
　なお、この単元では「慣性系」「非慣性系」という多くの学生に混乱を引き起こす用語を用いず、それぞれ「静止系」「加速系」で代用した。慣性系・非慣性系という語に興味がある人は10-01-1を参照されたい。
　ところで、大地に固定した座標系を「静止系」と呼んできたが、よくよく考えてみれば地球は自転や公転運動をしている。大地はむしろ「加速系」なのでは？という疑問も当然湧くと思う。それについては発展的学習内容ということで10-01-2に解説がある。参考にしてほしい。