1-30-2: 2次元の相対速度・加速度 ＜例題＞

1-30-1の1次元の相対速度・相対加速度を、２次元の場合に拡張します。　　

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

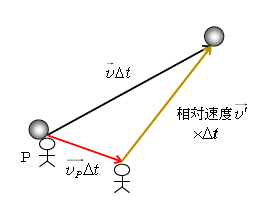
　図１には微小時間\(\Delta t\)の間の物体と観測者の変位が、それぞれ\(\vec{v}\Delta t, \, \vec{v_P}\Delta t \)と書かれている。すると\(\Delta t\)後の観測者から見て\(\Delta t\)後の物体は、黄色の矢印の向きに黄色の矢印の長さだけ動くように見える。ゆえに黄色の矢印の表しているものは、観測者から見た物体の相対速度\(\vec{v’}\)に\(\Delta t\)をかけたものである。この図１から、ベクトルの引き算で
　\(\vec{v’}=\vec{v}\)\(-\vec{v_P}\)
と表せることが言える。1-30-1の1次元の相対速度と同様に、Pから見た相対速度では\(\vec{v_P}\)を引き算するのだから、「から見た」(に対する)を引き算する公式と覚えよう。

　同様にPから見た物体の相対加速度も「から見た」を引き算する。
　\(\vec{a’}=\vec{a}\)\(-\vec{a_P}\)
　ここで、

例題　

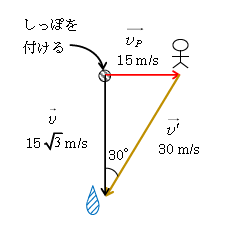
　雨が鉛直下向きに15\(\sqrt{3}\)m/sで降っているとする。水平な道路上を一定速度15m/sで走行している自動車から見て、雨はどちら向きにいくらの速さで落下するように見えるか。

解答・解説

　雨と観測者Pの速度をそれぞれ\(\vec{v} \,\vec{v_P}\)とすると、Pから見た雨の相対速度\(\vec{v’}=\vec{v}\)\(-\vec{v_P}\) 。ベクトルの引き算をするために\(\vec{v}\)と\(\vec{v_P}\)のしっぽ(矢印の根元)をくっ付けると、図２のような作図ができる。
　答　 車の進行方向と逆方向に鉛直から30°傾いた向き、速さ30m/s