1-35-2: 慣性力 ＜例題＞

1-33-1の「動く三角台」を題材に慣性力の実戦練習をしましょう！　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

例題　

　図のように、なめらかな水平面上に傾角\(\theta\)のなめらかな斜面を持つ質量\(M\)の三角台Ａが置かれ、水平方向に自由に動けるようになっている。いま台Ａの斜面上に質量\(m\)の小球Ｂをしずかに置き手を離すと、ＢはＡの斜面上をすべり降りた。Aの加速度の大きさを\(\alpha\)、重力加速度を\(g\)とする。
問１　台Aに固定した座標系から見たときに働く慣性力の向きと大きさを答えよ。
問２　小球Bが台Aから受ける垂直抗力の大きさ\(N\)を求めよ。
問３　BのAに対する相対加速度の大きさ\(\beta\)を求めよ。
問４　BがAの斜面上を距離\(l\)すべり下りる時間\(t\)を求めよ。

解答・解説

　やはり鉄則中の鉄則、1-08-1 : 力学攻略の基本　に沿って行こう。
問１　まず軸と力　図１のまずは座標軸から。台Aの運動は静止系から見るとする、すなわち左向きを正とする\(X\)軸及び\(Y\)軸を設定する。一方、問題文中の「台Aに固定した座標系」としては、台A上の観測者を想定しつつ、斜面に平行下向きの\(x\)軸及び\(y\)軸を取る。次に図１の力。特に慣性力(赤い矢印)について説明しよう。慣性力は1-35-1の通り公式(数式)的には\((-m\vec{A})\)だが、ポイントのように日本語で「向き」「大きさ」と押さえた方が、実際に問題を解くときは便利である。
　向き: 観測者の加速度\(\vec{A}\)と逆向き。図１の通り、台Aは斜め左向きに垂直抗力の反作用\(N\)を受けて、左向きに加速度\(\alpha\)(緑の矢印)で動く。つまり台A上の観測者の加速度も左向きに\(\alpha\)(赤い矢印)。それと逆向きに、慣性力の向きは
　　答　水平方向右向き　　（向きの答え方は1-04-1を参照のこと）
　大きさ: \(m|\vec{A}|\)。いま観測者の加速度\(\vec{A}=\vec{\alpha}\)だから、慣性力の大きさは
　　答　\(m\alpha\)
　・　この慣性力について、イメージ的な話を添えておこう。台Aを電車に例えると、電車が左向きに急加速すると、つり革が右向きに傾く。なぜなら慣性力が右向きに働くからである。

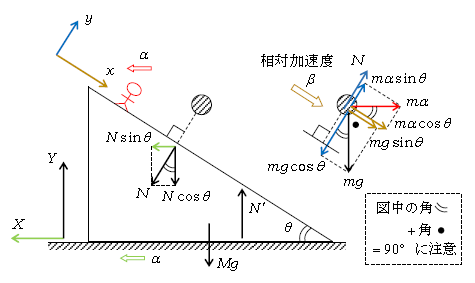
問２　次に\(ma=F\)　
　台A(\(X\)成分)　\(M\alpha=N\sin\theta \)　　　　　　　　　　(1)
　球B(\(x\)成分)　\(m\beta=mg\sin\theta+m\alpha\cos\theta \; \)　　　 (2)
　　　(\(y\)成分)　\(0=N+m\alpha\sin\theta-mg\cos\theta \)　　(3)
　（なお、台の\(Y\)成分について運動方程式を立てれば、水平面からの垂直抗力\(N’\)が求まるが、いまは不要ということであえて書かなかった。）
　(1)、(3)を見ると\(\alpha\)と\(N\)の連立になっている。\(\alpha\)を消去して\(N\)を求めよう。
　(1)より　\(\displaystyle \alpha=\frac{\sin\theta}{M} N\)　　　　　　　　　　　　　 (4)　　
　(3)に代入　\(\displaystyle 0=N+\frac{m\sin^2\theta}{M} N-mg\cos\theta \)
　∴　\(\displaystyle \frac{M+m\sin^2\theta}{M} N=mg\cos\theta \)　　∴　\(N=\)　答　\(\displaystyle \frac{Mm\cos\theta}{M+m\sin^2\theta} g \)
　[ 参考までに、この答は1-33-1の答と一致している ]

問３　まず(4)で\(\alpha\)を求め、それを(2)に代入して\(\beta\)を求めよう。
　問２の答の\(N\)を(4)に代入　\(\displaystyle \alpha=\frac{\sin\theta}{M} \frac{Mm\cos\theta}{M+m\sin^2\theta} g = \frac{m\sin\theta\cos\theta}{M+m\sin^2\theta} g \)
　(2)より　\(\displaystyle \beta=g\sin\theta+\alpha\cos\theta =g\sin\theta+\frac{m\sin\theta\cos^2\theta}{M+m\sin^2\theta} g\)
　　\(\displaystyle =g\sin\theta \cdot \left(1+\frac{m\cos^2\theta}{M+m\sin^2\theta} \right) \)
　　\(\displaystyle =g\sin\theta \cdot \frac{M+m\sin^2\theta \,\, +m\cos^2\theta}{M+m\sin^2\theta} =\)　　答　\(\displaystyle \frac{(M+m)\sin\theta}{M+m\sin^2\theta} g \)　
　　
問４　運動\(v,x\)を調べる　等加速度の公式を用いて
　\(\displaystyle l=\frac{1}{2}\beta t^2 \)　　∴　\(\displaystyle t=\sqrt{\frac{2l}{\beta}} \)
　問３の答を代入して　　\(t=\)　答　\(\displaystyle \sqrt{\frac{M+m\sin^2\theta}{(M+m)\sin\theta} \frac{2l}{g} } \)
　[ 参考までに、この答は1-33-2の答と一致している ]