1-28-1: 運動量と力積
「運動エネルギーと仕事」と対比して、「運動量と力積」いう重要な概念をきっちり理解しましょう!
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント
・ 運動量\(mv \) [\(\text{kg} \cdot \)m/s](\(m\): 質量、\(v\): 速度)
・ 力積\(I=Ft\) [N\(\cdot \)s](\(F\): 力、\(t\): 時間) ただし\(F\)一定のとき
\(F\)一定でないときは、力積\(I=F\)-\(t\)グラフの面積
・ 運動量変化=力積 \(mv-mv_0=I \)
この関係式は\(x\)成分、\(y\)成分別々に立てられる、すなわちベクトル式である。
\(m\vec{v} -m\vec{v_0}=\vec{I} \)
物体に一定の力\(F\)を時間\(t\)加え続ける状況を考えよう(図1)。
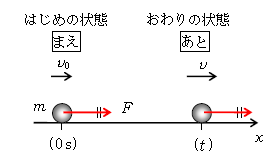
まず、運動量\(=\)\(mv\) と定義する(\(mv \)を運動量と呼ぶ、名付ける)。\(v\)が大きいほど、また\(m\)が大きいほど運動量は大きいことから、運動量はイメージ的にはものの勢いを表す。
力積\(I=\)\(Ft\) と定義する。力と時間の積に由来する名称。
また、運動量変化= (あとの運動量) - (まえの運動量)
= \(mv\) - \(mv_0\)
と定義する。このように定義すると、
運動量変化=力積 つまり、
\(mv -mv_0=I \) (1)
が成り立つことを以下のように証明できる。
証明 等加速度の公式\(v=v_0+at \) (2)
を両辺\(m\)倍 \(mv -mv_0=mat\)
右辺に運動方程式 \(ma=F\)(図1)を代入
\(mv -mv_0=Ft=I \) よって(1)が証明された
1-05-1でやった通り、運動方程式 \(ma=F\)は右辺が原因、左辺が結果を表し、「力\(F\)という速度変化の原因によって、結果的に加速度\(a\)が生じる」という読み方ができた。(1)式も右辺が原因、左辺が結果を表し、「物体に力積(力と時間の積、右辺、原因)が加わると、物体の運動量\(mv\) が変化する(左辺、結果)」と読める。ところで運動量は\(v\)に比例しているから、「運動量\(mv\) が変化する」とは結局「速度が変化する」「加速度が生じる」という意味である。
(1)式が特に有用であるのは、\(F\)が一定でない、例えば図2の青線のグラフのような場合。ここで、1-02-1で \(v\)-\(t\)グラフの面積=変位 を証明するときに用いた、階段グラフの方法を使おう。
横軸の\(0~t\)を\(\Delta t \)ごとに区切って、\(F\)が階段状に変化していくとする。図2では5等分したが、最終的には無限個等分し、階段グラフを青線のグラフに限りなく近づける。
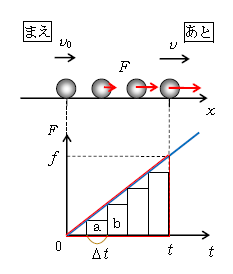
まず、長方形aにおいては \(F\)=長方形のタテの長さ が一定だから、
\(F\)-\(t\)グラフの面積=\(F\Delta t\)=力積
が成り立つ。つまりaの面積は、最初の\(\Delta t\)での力積に等しい。
同様に、bの面積は次の\(\Delta t\)での力積に等しい、・・・。
全ての長方形を足した階段グラフの面積は、\(0~t\)での力積の合計に等しい。
従って、\(0~t\)の\(F\)-\(t\)グラフの面積=図2の赤の直角三角形の面積=\(0~t\)での力積\(I\)。つまり、\(F\)が変化していく場合、\(F\)-\(t\)グラフの面積=力積\(I\) となることが言えた。
∴ \(\displaystyle I=t \cdot f \cdot \frac{1}{2} =\frac{1}{2} ft \)
すると(1)より \(\displaystyle mv-mv_0=I=\frac{1}{2} ft \)
∴ \(\displaystyle v=v_0+\frac{ft}{2m} \) (3)
ここで仮に等加速度の公式(2)を使って\(v\)を求めようとすると、「待てよ、加速度\(a\)の値は?」と手が止まってしまうだろう。なぜなら\(0~t\)の間に\(F=0~f\)まで変わるのだから、運動方程式\(ma=F\)にどの\(F\)を代入すればよいのかという問題が生じている。例えば\(F=f\)を代入すると、\(\displaystyle a=\frac{f}{m} \) 。これと(2)から \(\displaystyle v=v_0+\frac{f}{m} t \) となって、答が(3)と合わない。そもそも今\(F\)が\(0~f\)と変わるにつれて、\(\displaystyle a=\frac{F}{m} \)が\(\displaystyle \frac{0}{m}~\frac{f}{m} \)と変わるから、「等」加速度運動ではない。よって等加速度の公式はハナから使えないのである。
ところが(1)の運動量と力積の関係は ―― たとえ等加速度運動でなくても、力積(\(F\)-\(t\)グラフの面積)を計算することによって、まえの\(v_0\)からあとの\(v\) を求めることができるところが強味だ。
再び図1に戻って ―― \(v_0,v\)が実は\(x\)-\(y\)平面内を運動する物体の速度の\(x\)成分\(v_{0x},v_x\)のことで、 \(F\)も実は力の\(x\)成分\(F_x\)のことだったとしよう。\(I_x=F_x t\)とすると、先の証明と全く同様にして
\(mv_x -mv_{0x}=I_x \) (4)
が成り立つことが言える。また、\(F_x\)が一定でない場合は\(I_x\)=\(F_x\)-\(t\)グラフの面積であることも図2と同様にして示せる。さらに\(y\)成分についても同様に
\(mv_y -mv_{0y}=I_y \) (5)
が言える。よって、運動量と力積の関係は\(x\)成分、\(y\)成分別々に立てられることが分かる。
(4),(5)をまとめて \(m(v_x,v_y)-m(v_{0x},v_{0y})=(I_x,I_y) \) のように書けるから、結局運動量と力積の関係はベクトル式
\(m\vec{v} -m\vec{v_0}=\vec{I} \) であることも言える。
最後に単位を確認しておこう。
運動量\(mv \)の単位は [\(\text{kg} \cdot \)m/s]
力積\(I=Ft\)の単位は [N\(\cdot \)s]
(1)の等号が成り立つことから運動量と力積の単位は等しいはず。じっさい、[N\(\cdot \)s=\(\text{kg} \cdot \)m/s\(^2\)\(\cdot \)s=\(\text{kg} \cdot \)m/s]となって等しい。


