1-02-1: v-tグラフ

v-tグラフは物理のスタートラインです。 →　＜例題＞は1-02-2へ 　　　　　　　　　　　　　　　　　　　　　　　　　　　

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

　図１の青い曲線は縦軸が\(v\)軸、横軸が\(t\)軸の\(v\)-\(t\)グラフの例。

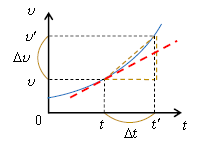
　図1縦軸の速度変化\(\Delta v\)［m/s］を横軸の時間\(\Delta t\)[s]で割ったもの\(\displaystyle \frac{\Delta v}{\Delta t} \)[m/s\(^2\)] を平均加速度という。\(\Delta v \div \Delta t\)は点線の直角三角形の斜辺の傾きに等しい。1-01-1と同様に、\(\Delta t\)を限りなく小さく取ると、瞬間加速度あるいは単に加速度\(a\)という。
　　加速度\(\displaystyle a=\frac{\Delta v}{\Delta t} \) 　（ただし\(\Delta t→ 0\)）　　(1)
\(\Delta t\rightarrow 0 \)にすると、\(\Delta v \div \Delta t \)斜辺の傾きは、接線の傾きに限りなく近づくから、加速度\(a\)は\(v\)-\(t\)グラフの接線の傾きに等しい。

　「なぜ\(\Delta v\)を\(\Delta t\)で割ると加速度になるのか」と聞かないでほしい。むしろ、\(\Delta v\)を\(\Delta t\)で割ったものを加速度と呼ぶ、名付ける、決めているのである。この「呼ぶ・名付ける・決める」タイプの式のことを定義式という。1-01-1の(1)式は速度の定義式、 すぐ上の(1)式は加速度の定義式。
　ではなぜそのように定義するのか。定義しておくと役に立つからである。例えば\(a\)は、1-04-1: 落体の運動 や1-05-1: 運動方程式 以降の単元で役に立つことになる。
　(1)の\(\displaystyle \frac{\Delta v}{\Delta t} \)は「1sあたりの速度変化」という意味だから、加速度2m/s\(^2\)とは、速度が1sあたり2m/sずつ増えて0,2,4m/s,\(\cdots \)のように加速していくという意味。本当はもっと正確に言うと、例えば0.00001s間に0.00002m/s増えるということなので、念のため。
　ところで、速さ(速度の絶対値)の大小は速い遅いを表す。一方、加速度の大きさ(加速度の絶対値)は速度が(1sあたりに)どれだけ変化するかの大小を表す。たとえ遅い物体であっても、その速度が(1sあたりに)大きく変化しているならば、加速度の大きさは大きい。
　加速度\(a\)も符号・向きを持つ。\(a=-\)3m/s\(^2\)とは、速度が1sあたり3m/s減って減速するという意味。

　次なる重要事項として、\(v\)-\(t\)グラフの面積は変位に等しい。それを図２を用いて証明しよう。横軸の\(0～t\)を \(\Delta t\)ごとに区切って、あえて速度\(v\)が階段状に増えていくと考えてみる。図2では\(0～t\)を5等分したが、もっと細かく100万等分、さらには無限個等分すれば、階段グラフは青い曲線のグラフ(実際の運動のグラフ)に限りなく近づくから、正確に運動を考察できる。　

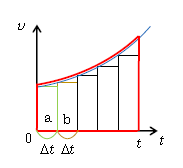
　さて、最初の長方形aの面積はタテ(速度)×ヨコ(時間)　だから図2横軸の一番左の\(\Delta t\)の間の変位に等しい。次の長方形bの面積は次の\(\Delta t\)の間の変位に等しい、･･･。そこで、全ての長方形を足した階段グラフの面積は、\(0～t\)の変位の合計に等しい。従って\(0～t\)の\(v\)-\(t\)グラフの面積（赤線で囲まれた部分）は、\(0～t\)の変位に等しい。よって証明された。
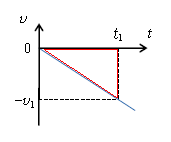
　ところで、図３のように横軸の下側に表れる\(v\)-\(t\)グラフでは、縦軸の\(v\)の値が負である。1-01-1で述べた通り、速度\(v\)の向きは運動の向きに等しいから、変位は負の向き。つまり、横軸の下側の\(v\)-\(t\)グラフの面積は負の値であると決めておけば変位に等しい。図３の赤い三角形の面積より、
　\(0～t_1\)の変位\(\displaystyle =-t_1×v_1÷2=-\frac{1}{2}v_1t_1 \) となる。