1-18-2: 弾性力と力学的エネルギー保存則 <例題>
少し長めの例題。ここは踏ん張りどころと思って頑張りましょう!
例題
図のように、床に高さ\(2h\)のスタンドを置き、質量が無視できる自然の長さ\(h\)のゴムひもを点Aに取り付ける。ゴムひもの他端に質量\(m\)の小球を取り付けて、点Aから小球を静かに離すと、小球は鉛直に落下し、床に衝突せずに再び上昇した。ここで、ゴムひもの弾性力は、ゴムひもが自然の長さから伸びた場合にのみ働き、その大きさは自然の長さからの伸びに比例するものとし、その比例定数を\(k\)とする。ただし、重力加速度の大きさを\(g\)とする。
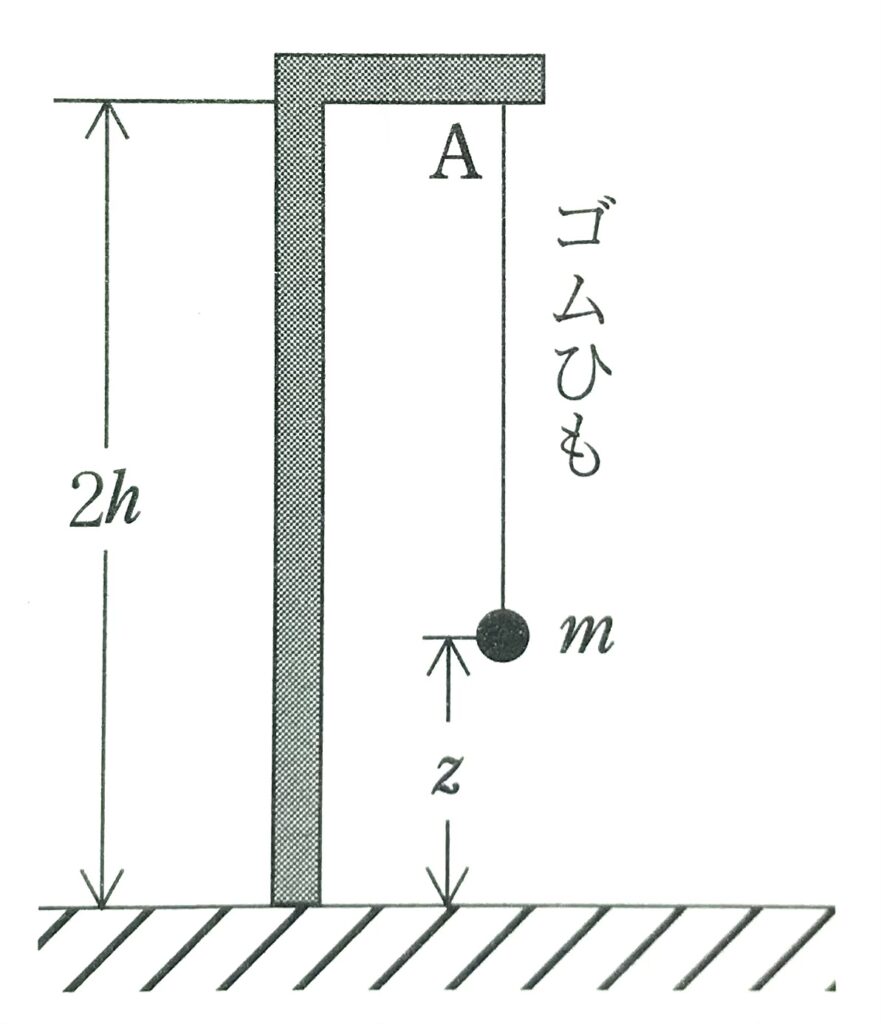
問1 小球が高さ\(h\)の位置を最初に通過したときの、小球の速さはいくらか。正しいものを、次の①~8のうちから一つ選べ。
① \(\displaystyle \sqrt{\frac{gh}{2} } \) ② \(\displaystyle \sqrt{gh} \) ③ \(\displaystyle \sqrt{2gh} \) ④ \(\displaystyle 2\sqrt{gh} \)
⑤ \(\displaystyle \sqrt{\frac{h}{2g} } \) ⑥ \(\displaystyle \sqrt{\frac{h}{g} } \) ⑦ \(\displaystyle \sqrt{\frac{2h}{g} } \) ⑧ \(\displaystyle 2\sqrt{\frac{h}{g} } \)
問2 高さが\(z\)(\(z<h\))のときの小球の加速度\(a\)はいくらか。正しいものを、次の①~⑦のうちから一つ選べ。ただし、加速度\(a\)は鉛直上向きを正とする。
① \(\displaystyle \frac{k}{m} z-g \) ② \(\displaystyle \frac{k}{m} (h-z)-g \) ③ \(\displaystyle \frac{k}{m} (h+z)-g \)
④ \(-g\) ⑤ \(\displaystyle \frac{k}{m} z \) ⑥ \(\displaystyle \frac{k}{m} (h-z) \) ⑦ \(\displaystyle \frac{k}{m} (h+z) \)
問3 小球が最下点に達したときの高さを\(z_0\)とするとき、比例定数\(k\)を表す数式として正しいものを、次の①~⑥のうちから一つ選べ。
① \(\displaystyle mg\frac{z_0}{(h-z_0)^2} \) ② \(\displaystyle 2mg\frac{z_0}{(h-z_0)^2} \) ③ \(\displaystyle mg\frac{2h-z_0}{(h-z_0)^2} \)
④ \(\displaystyle 2mg\frac{2h-z_0}{(h-z_0)^2} \) ⑤ \(\displaystyle mg\frac{1}{h-z_0} \) ⑥ \(\displaystyle 2mg\frac{1}{h-z_0} \)
解答・解説
ゴムは自然長より伸びたなら、ばね同様に扱える → 問2
たるんでいるときは、何もないのと同様に扱える(たるんだゴムは力を及ぼしてこない)→ 問1
問1 単に速さを求める、時間を求めなくてよい問題なので、エネルギーの考え方を用いる(1-17-1)。
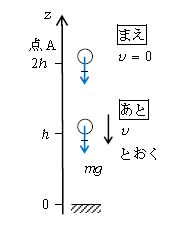
重力・弾性力以外の力がないので、力学的エネルギー保存(1-17-1)を立てる(図1)。
あと = まえ
\(\displaystyle \frac{m}{2} v^2 +mgh = \frac{m}{2} 0^2 +mg2h \)
∴ \(\displaystyle \frac{m}{2} v^2 =mgh \) ∴ \(v=\sqrt{2gh} \) 答 ③
問2 加速度を求めたいので、運動方程式を立てる。ところで、弾性力\(|F|=k|x|\)、弾性エネルギー\(\frac{k}{2} x^2 \)というときの\(|x|\)は、自然長からののび・ちぢみのこと。
弾性力 \(|F|=k\)×(のび・ちぢみ)、
弾性エネルギー \(\frac{k}{2} \)×(のび・ちぢみ)\(^2\) と日本語で覚えておくと問題に対処しやすい。
1-08-1: 力学攻略の基本 の流れに沿って行こう。
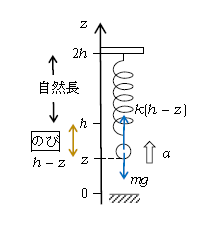
まず軸と力 図2に (のび) \(=h-z\) と示した。
(のび・ちぢみとは、言いかえると自然長からのずれの長さなので、自然長の位置\(h\)と小球の位置\(z\)の差を取る。\(z<h\)なので、大きい\(h\)から小さい\(z\)を引いて、のび>0になるようにする。)
\(|F|=k\)×(のび・ちぢみ)\(=k(h-z)\) (\(|F|=kz\)とはならないので注意)
次に\(ma=F\) 問2に「加速度\(a\)は鉛直上向きを正」と指定されたので、上向きに\(a\)と図示する(求まった\(a\)が負なら、実は下向きだったと後で解釈すればよい)。
\(ma=k(h-z)-mg\) ∴ \(\displaystyle a=\frac{k}{m}(h-z)-g \)
答 ②
問3 「最下点に達する」のはのび最大のときだから、1-18-1図4にある通り\(v=0\)のとき。このときの高さが\(z_0\)ということは、「速さ\(v=0\) のとき位置\(z=z_0\)になる」という条件の下、\(k\)を求める問題だと読み取れる。「速さ」と「位置」の関係が与えられ、しかも時間を求めなくてよいのだから、エネルギーで解こう(1-17-1)。
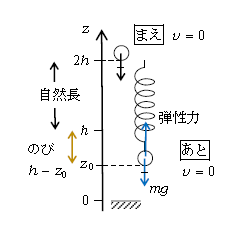
重力・弾性力以外の力がないので、力学的エネルギー保存(1-17-1)を立てる(図3)。
「まえ」を\(z=2h\)に取る。(\(z=2h\)では運エネ=0なので簡単。\(z=h\)では運エネ\(\ne 0\)なので面倒)。
[ 計算が簡単になるように「まえ」を選ぼう ]
もちろん位置エネルギーは\(mg\)×(高さ)と\(\frac{k}{2} \)×(のび・ちぢみ)\(^2\)の2種類。
あと = まえ
\(\displaystyle \frac{m}{2} 0^2 +mgz_0+\frac{k}{2} (h-z_0)^2 = \frac{m}{2} 0^2 +mg2h+0 \)
[ ゴムはたるんでいると何もないのと同じだから、まえの弾性エネルギーはない ]
∴ \(\displaystyle \frac{k}{2} (h-z_0)^2=mg(2h-z_0) \)
∴ \(\displaystyle k=2mg \frac{2h-z_0}{(h-z_0)^2} \) 答 ④
<補足> 問3で考えた最下点は、運動中にいったん止まって\(v=0\)になる位置。これはつり合いの位置ではない。なぜなら、最下点では小球はゴムの弾性力に引かれてすぐに上昇し出す、つまり小球に働く合力が0ではない位置だから。
つり合いの位置とは1-05-1の通り合力0の位置。言いかえると小球を手で支えながら運んで手を離してもそのまま\(v=0\)でとどまる位置のこと(合力0なので)。
「つり合いの位置を求めよ」とあったら、つり合いの式で求める。具体的には問2と同様に
\(m0=k(h-z)-mg\) ∴ \(\displaystyle z=h-\frac{mg}{k} \)
一方、つり合いの位置は力学的エネルギー保存では求まらない。なぜなら、つり合いの位置に持ってくるまでに、手の力 ―― 重力・弾性力以外 ―― が仕事をして力学的エネルギーが変化するから(1-17-2)。


