1-16-3: 2次元の運動エネルギーと仕事(続き)
2次元での運動エネルギーと仕事の関係は、1次元の場合を一般化したもの、それをしっかり押さえましょう。
→ 関連事項はは10-04-1: 力学的エネルギー保存則 の証明へ
ポイント (式の説明は本文を参照のこと)
・ 運動エネルギー \(\displaystyle K=\frac{m}{2}|\vec{v}|^2 \)
仕事 \(\displaystyle W=\lim_{\Delta \vec{r}→0} \sum_{\Delta \vec{r}} |\vec{F}|\cos\phi \cdot |\Delta \vec{r}| \)
・ 運動エネルギー変化 = 仕事
\(\displaystyle \frac{m}{2}|\vec{v}|^2- \frac{m}{2}|\vec{v_0}|^2 \) \(=\) \(\displaystyle W=\lim_{\Delta \vec{r}→\vec{0}} \sum_{\Delta \vec{r}} |\vec{F}|\cos\phi \cdot |\Delta \vec{r}| \)
この式は\(x\)成分の式、\(y\)成分の式のように別々に立ててはいけない
1-16-2最後の式 \(\displaystyle \Delta \left( \frac{m}{2}|\vec{v}|^2 \right) =|\vec{F}|\cos\phi \cdot |\Delta \vec{r}| \) ただし\(\Delta \vec{r}→ \vec{0} \) (1)
(\(\phi\)は\(\vec{F}\)と\(\Delta \vec{r}\)のなす角) をこの単元の出発点とする。
図1のような曲線の軌道を\(n\)個の線分(黄色)に分割し、それぞれを変位\(\Delta \vec{r_1},\Delta \vec{r_2}, \cdots, \Delta \vec{r_n} \)と名付ける。最終的には\(\Delta \vec{r_k}→\vec{0}\)(\(k=1,2,\cdots,n\))の極限を取るから、線分ごとの運動と曲線運動は一致する。\(k\)番目の拡大図が図2。これに(1)を適用すると、
\(\displaystyle \frac{m}{2}|\vec{v_k}|^2- \frac{m}{2}|\overrightarrow{v_{k-1}}|^2 = |\vec{F_k}|\cos\phi_k \cdot |\Delta \vec{r_k}| \; \) (2)
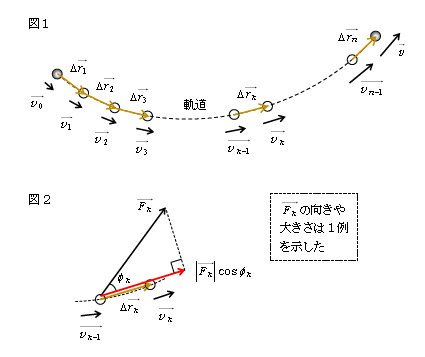
再び図1に戻って、(2)を\(k=1,2,3,\cdots,n\)番目について書くと、
\(\frac{m}{2}|\vec{v_1}|^2- \frac{m}{2}|\vec{v_0}|^2 = |\vec{F_1}|\cos\phi_1 \cdot |\Delta \vec{r_1}| \) [ \(\vec{F_1},\phi_1\)は図示していない ]
\(\frac{m}{2}|\vec{v_2}|^2- \frac{m}{2}|\vec{v_1}|^2 = |\vec{F_2}|\cos\phi_2 \cdot |\Delta \vec{r_2}| \)
\(\frac{m}{2}|\vec{v_3}|^2- \frac{m}{2}|\vec{v_2}|^2 = |\vec{F_3}|\cos\phi_3 \cdot |\Delta \vec{r_3}| \)
\(\cdots \cdots \cdots\)
\(\frac{m}{2}|\vec{v}|^2- \frac{m}{2}|\overrightarrow{v_{n-1}}|^2 = |\vec{F_n}|\cos\phi_n \cdot |\Delta \vec{r_n}| \)
これら\(n\)個の式を足すと、左辺が数学の「部分分数分解」のようにして\(\frac{m}{2}|\vec{v}|^2- \frac{m}{2}|\vec{v_0}|^2 \) となり、右辺は和の記号を用いて書けるから、結局次のようになる。
\(\displaystyle \frac{m}{2}|\vec{v}|^2- \frac{m}{2}|\vec{v_0}|^2 =\sum_{k=1}^{n} |\vec{F_k}|\cos\phi_k \cdot |\Delta \vec{r_k}| \) (*)
物理では、添え字\(k\)を省き、さらに和の記号も\(\displaystyle \sum_{\Delta \vec{r}} \)のように書いて、右辺を\(\displaystyle \sum_{\Delta \vec{r}}|\vec{F}|\cos\phi \cdot |\Delta \vec{r}| \) のように略記することが多い。
ここで\(\Delta \vec{r}→\vec{0}\)の極限を取っていたことを思い出そう。\(\Delta \vec{r}→\vec{0}\)での(*)の右辺を仕事\(W\)と定義(1-02-1)する。
\(\displaystyle W=\lim_{\Delta \vec{r}→\vec{0}} \sum_{\Delta \vec{r}}|\vec{F}|\cos\phi \cdot |\Delta \vec{r}| \)\(\;\) (3)
すると(*)より、
\(\displaystyle \frac{m}{2}|\vec{v}|^2- \frac{m}{2}|\vec{v_0}|^2 \) \(=\) \(\displaystyle W=\lim_{\Delta \vec{r}→\vec{0}} \sum_{\Delta \vec{r}} |\vec{F}|\cos\phi \cdot |\Delta \vec{r}| \) (4)
これが 運動エネルギー変化 = 仕事 の式である。
(3)を見ると、\(|\vec{F}|\cos\phi\)は図2より力\(\vec{F}\)のうち物体の移動方向\(\Delta \vec{r}\)に沿う成分。\(|\Delta \vec{r}|\)は微小な距離。ゆえに(3)の2次元運動の仕事\(W\)は「(力の移動方向成分)×(微小距離)を足し上げたもの」というような意味になる。これは、1-16-1の単純な1次元運動の仕事\(W\)=(力の移動方向成分)×(距離)を一般化したものになっている。
また、振り返ってみれば(4)を導くのに用いたのは、運動エネルギー\(K\)と仕事\(W\)の定義、運動方程式\(\displaystyle m\frac{d\vec{v}}{dt}=\vec{F} \)、及び数式変形のみである。
この(4)を押さえれば、10-03-2: 位置エネルギー の本格的な説明や、10-04-1: 力学的エネルギー保存則の証明 などへと話が広がっていく。
さて、1-16-2の通り2次元の運動エネルギー\(K\)は定義により\(\displaystyle K=\frac{m}{2}|\vec{v}|^2 \)\(\displaystyle =\frac{m}{2}({v_x}^2+{v_y}^2) \) だった。ということは、\(K\)には\(v_x\)と\(v_y\)両方を含めなければならない。言い換えると、(4)は\(x\)成分の式、\(y\)成分の式のように別々に立ててはいけない。とりわけ左辺は、速さ\(|\vec{v}|\)(や\(|\vec{v_0}|\))丸ごとの2乗をとるのだ。
運動方程式\(m\vec{a}=\vec{F}\)のように、\(x\)成分の式\(ma_x=F_x\) と\(y\)成分の式\(ma_y=F_y\)を別々に立てられるのを「ベクトル式」という。これに比して、(4)のように別々に立ててはいけないのは「スカラー式」という。もう気付いている人もいるだろうが、(4)の左辺に現われる\(\vec{v}\)の大きさ\(|\vec{v}|\)は数学的にはスカラー量である。また、(4)の右辺の\(|\vec{F}|\cos\phi \cdot |\Delta \vec{r}|\)は内積\(\vec{F} \cdot \Delta \vec{r} \)と書き換えられ(1-16-2の冒頭の(☆)参照)、内積もまた数学的にはスカラー量である。ゆえに(4)はスカラー式となる。エネルギーも仕事も、ベクトル量ではなくスカラー量である。
<補足> (4)の右辺の仕事を大学では \(\displaystyle W=\int_C \vec{F} \cdot d\vec{r} \) のように書く。\(\displaystyle \int_C \) は「線積分」の記号で、「(曲線)軌道\(C\)に沿って積分せよ」というほどの意味。


