1-17-1: 力学的エネルギー保存則 ー 力学攻略の基本 第2弾
力学的エネルギー保存則は力学の中で格段に重要度が高い法則。きっちり理解しましょう! → 力学的エネルギーの変化 は1-17-2へ、力学的エネルギーの保存と変化<例題> は1-17-3へ、力学攻略の基本 第1弾は1-08-1へ
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント
・ 重力による位置エネルギー=\(mg\)×(高さ)[J]
・ 弾性力による位置エネルギー=\(\displaystyle \frac{k}{2} \) ×(のび・ちぢみ)\(^2\)(次の1-18-1で扱う)
・ 力学的エネルギー = 運動エネルギー + 位置エネルギー
・ 力学的エネルギー保存則
重力・弾性力のみが仕事をするときには、力学的エネルギーは一定のまま
ポイント (このページの最後に再掲します)
・ 時間を求めたいときは まず軸と力、次に\(ma=F\)、\(v,x\)を調べる
・ 単に速さ・位置を求めたい、時間を求めなくてよいときはエネルギー
まずは定義から。(1-02-1でやった通り、「○○と呼ぶ・名付ける・決める」タイプの式を定義式という。名付けておくと役に立つから定義するわけである。)
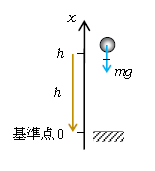
重力による位置エネルギー(図1)
=基準点からの高さ\(h\)の所にある物体に対して、基準点まで重力がすることのできる仕事
=(力の移動方向成分)×(距離)= \(mg\)×(高さ)\(h\)
(つまり、基準点とは高さ0と決めておく点。とりあえず決めておくだけの点なので、基準点は別に図1のように地面の高さになくてもよい(例えば上空でもよい)。)
力学的エネルギー= 運動エネルギー + 位置エネルギー
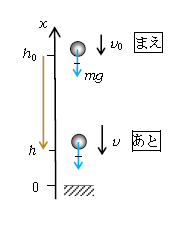
こう定義すると、例えば図2のような落体の運動で次のことが成り立つ(すぐに証明する)。
あとの力学的エネルギー = まえの力学的エネルギー つまり
あとの運エネ + 位エネ = まえの運エネ + 位エネ つまり
\(\displaystyle \frac{m}{2} v^2 \: \) + \(mgh \) = \(\displaystyle \frac{m}{2}
{v_0}^2\) + \(mgh_0 \) (✩)
つまり、力学的エネルギー=一定。物理では、ある量が時間的に一定のままであること(すなわち、あと=まえ になること)を「保存する」と表現するから、これを力学的エネルギー保存則と言う。
(✩)式の証明には、1-16-1でやった(運動エネルギー変化=仕事)、すなわち
\(\frac{m}{2} v^2- \frac{m}{2} {v_0}^2 =W \) (1)
を用いる。図2で
仕事\(W=\)(力の移動方向成分)×(距離)
\(=mg×(h_0-h)=mgh_0-mgh \) (2)
(変位と距離の違いに注意。変位\(\Delta x\)=あと-まえ=\(h-h_0<0\)は符号を持つ量だが、距離=\(|\Delta x| =h_0-h >0\)は符号を持たない。)
(2)を(1)に代入して \(\frac{m}{2} v^2- \frac{m}{2} {v_0}^2 =mgh_0-mgh \)
∴ \(\frac{m}{2} v^2+mgh= \frac{m}{2} {v_0}^2 +mgh_0 \) よって(✩)が証明された。
物体の運動中、運動エネルギー\(\frac{m}{2} v^2 \)も位置エネルギー\(mgh\)も各々は値が変わっていくのに、それらの合計は一定のままだというのが面白い。位置エネルギー\(mgh\)が減れば、運動エネルギー\(\frac{m}{2} v^2 \)が増えてそれらの合計は一定とも言える。つまり高さ\(h\)が減ると速さ\(v\)が増える(逆に\(h\)が増えれば\(v\)は減る)。
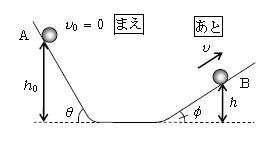
エネルギー保存則の威力を実感するために、図3で、点Aを初速度0で出発した物体が点Bを通過するときの速さ\(v\)を求めてみよう(摩擦はないとする)。今まで通りまず軸と力、次に\(ma=F\)、\(v,x\)を調べるとやるのは面倒だ。しかし、証明はしないが結論だけを述べると、エネルギー保存則は鉛直方向の運動だけでなく、運動方向によらず成り立ち、物体がカーブを描くような曲線運動でさえも成り立つ。とりわけ、\(v\)がどちらを向いていようが、ともかく運動エネルギーは速さ\(v\)を用いて\(\frac{m}{2} v^2\)と計算すればよい(この証明について学びたい人は、まず次の単元1-17-2の最後の段落を参照のこと)。すると(✩)より
あと = まえ
\(\displaystyle \frac{m}{2} v^2+mgh= \frac{m}{2} 0^2 +mgh_0 \)
このようにして、図3でたった1つの式で\(v\)が求まる。
∴ \(\displaystyle \frac{m}{2} v^2 =mg(h_0-h) \) ∴ \(v^2 =2g(h_0-h) \)
∴ \(v =\sqrt{2g(h_0-h)} \)
(なお、本当は速さは、速度\(v\)に絶対値を付けて速さ\(|v|\)と書くべきなのだが、略して速さ\(v\)と書いてしまうことも多いから、念のため。)
ともかく、なぜこんなに簡単に速さが求まったのかと言えば、エネルギー保存則(✩)の中に\(v\)(速さ)と\(h\)(高さすなわち位置)が入っているからだ。速さや位置を求めるならエネルギーに限る。運動方程式は面倒だ。ただし、エネルギー保存則の中には「時間」が入っていない。ということは、エネルギー保存則では時間は計算できない。「時間を求めよ」という問題に対しては、運動方程式の流れで行くしかない。結局、運動方程式とエネルギーは、次のようにして使い分けるとよい。
ポイント
・ 時間を求めたいときは まず軸と力、次に\(ma=F\)、\(v,x\)を調べる
・ 単に速さ・位置を求めたい、時間を求めなくてよいときはエネルギー


