1-24-1: 単振動の時間変化の調べ方 ー 力学攻略の基本 第3弾

単元1-27までで力学の3分の2は終了したと言えます。あと一息！タイトルの「時間変化を調べる」とは時刻tの位置x,速度vを求めること。それは1-08-1「力学攻略の基本」を押さえることに過ぎません。　

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

　このように単振動では、1-08-1に沿ったまとめもやや長くなる。しかし、これを押さえるだけで「単振動が面白いように解けるようになった」「単振動って実は簡単ですね」と、多くの学生が喜びの表情で私に報告してくれている。ぜひ踏ん張り所だと思って頑張ってほしい。
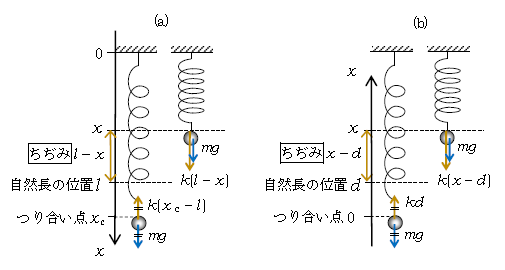
　1-22-1で扱った鉛直方向のばねを題材にしよう、それが図1(a)。
　まず軸と力　ポイントに示した通り、\(x\)軸に正の向き、原点、自然長の位置、つり合い点\(x_c\)（合計4つ）を添え、さらに\(x_c\)及び任意の位置\(x\)に物体を書く（図を2つ書く）。
　1-22-1で確認した通り、のび・ちぢみいずれか一方だけ調べればよいから、例えばばねの縮んでいる状態を図示した。
　ここで学習効果を狙って、\(x\)軸を上向きに取り直し、原点をつり合い点に取る、それが図1(b)。つり合い点までのばねののびを\(d\)とおくと、自然長の位置は\(d\)と表せる。一方、位置\(x\)でのちぢみ(自然長からのずれの長さ)は\(x-d\)（上向きを正にとると座標\(x\)の方が\(d\)より大きく、大きい方から小さい方を引いた\(x-d\)がちぢみの長さとなる）、ゆえに弾性力は\(k(x-d)\)である。

　次に\(ma=F\)　図1(a)のパターンの運動方程式は1-22-1で立てたから、(b)のパターンを扱う。
　つり合いの式：\(0=kd-mg\)
　任意の\(x\)での運動方程式：\(ma=-k(x-d)-mg=-kx+kd-mg=-kx\)
　　　　　　　　　　　　　　　[すぐ上のつり合いの式を用いた]
　　　　　　　∴　\(\displaystyle (a=)\frac{d^2x}{dt^2} =-\frac{k}{m} (x-0) \)
　これを単振動の方程式　\(\displaystyle \frac{d^2x}{dt^2} =-\omega^2 (x-x_c) \)　と比べて
　 \(\omega\) \(\displaystyle =\sqrt{\frac{k}{m}} \) 、 \(x_c\) \(=0\) を読み取る（元々原点をつり合い点に取ったのだから、\(x_c=0\)になるのは当然である）。少し補足をしておくと、加速度\(\displaystyle a=\frac{d^2x}{dt^2} \)は1sあたりの速度の変化だから、平たく言うなら速くなったり遅くなったりの様子を定める量。加速度が定数なら等加速度運動。一方、加速度\(\displaystyle \frac{d^2x}{dt^2} =-\omega^2 (x-x_c) \)の形（これは1-22-1でやった通り単振動の方程式・定義式である）になったら、単振動である証拠なのだ。
　運動\(v,x\)を調べる　単振動では1-23-1の通り、必ず\(x=A\sin(\omega t+\phi)+x_c\)（\(t\)の三角関数）となる。くれぐれも、等加速度の公式\(x=x_0+v_0t+\frac{1}{2}at^2\)（\(t\)の2次関数）のようにはならない。この運動\(v,x\)を調べるの具体的な説明は、次の単元1-24-2に回すことにする。

　なお1-23-1でやった通り、周期\(\displaystyle T=\frac{2\pi}{\omega} \)だから、
　　\(\displaystyle T=2\pi \sqrt{\frac{m}{k}} \)
つまり、運動方程式を立てて\(\omega\)を読み取るだけで即座に周期が分かる。\(T=2\pi \sqrt{\frac{m}{k}} \)は極めて出題率の高い公式だから、ぜひ覚えておきたい。分子の\(m\)を「ミ」と読み、分母の\(k\)を「カン」と読んで、「ミカンの公式」と言ったりもする（昭和の頃からあるネーミングのようだ）。