1-26-1: 単振動独特のエネルギー保存則
このエネルギー保存則を使いこなせるようになれば、物理の力もかなり付いたと言えます!
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント
・ 運動方程式が \(ma=-K(x-x_c)\) の形になったなら、
エネルギー保存則は \(\displaystyle \frac{m}{2}v^2+ \frac{K}{2}(x-x_c)^2=\)一定 となる。
1-22-1でやった通り、単振動の方程式 \(a=-\)〇(\(x-\)□) (1)
は、単振動の定義式でもあった。つまり、単振動という現象を扱う限り、必ず(1)式が成り立っているということである。ここで、〇\(=\)(角振動数\(\omega)^2 \)で、□\(=x_c\)はつりあいの位置である。
(1)の両辺を\(m\)倍して\(K=m\omega^2 \)とおけば
\(ma=-K(x-x_c) \, \) (2)
単振動の定義式(1)を\(m\)倍しただけだから、単振動という現象を扱う限り、必ず運動方程式は(2)の形になることは明白である。
さて、(2)運動方程式の右辺は合力\(F\)を表す。ここで\(F=-K(x-x_c)\)は弾性力だけ(水平方向のばね)の場合もあるし、弾性力と重力の合力(鉛直方向や斜面方向のばね)になることもある。また、\(F=-K(x-x_c)\)が浮力と重力の合力(弾性力なし)になることもあるし、クーロン力だけの場合もある。つまり、弾性力が関与しない場合もあるので\(K\)はばね定数とは限らず、(2)の1行上に示した通り\(m\omega^2 \)という量を単に1文字で\(K\)と表したものにすぎない。ともかく、弾性力なしでも、単振動という現象を扱う限り、必ず合力\(F=-K(x-x_c)\)と表せることが重要である。
タイトルの「単振動独特のエネルギー保存則」を導くために、1-16-1の
運動エネルギー変化=仕事 \(\displaystyle \frac{m}{2} v^2 -\frac{m}{2} {v_0}^2=W \)
の関係式を用いよう。さらに、力\(F=-K(x-x_c)\)の大きさが\(x\)とともに変わって一定ではないので、1-18-1でやった
\(F\)-\(x\)グラフの面積=仕事\(W\) も用いる。
図1では\(x\)軸を水平方向に書いたが、鉛直や斜面方向の運動(例えば斜面方向の単振動)では\(x\)軸を鉛直や斜面方向に想定していることに注意したい。グラフの縦軸は合力\(F=-K(x-x_c)\)に取った。ゆえに横軸\(x\)が\(x_c,x_1,x_2\)の所に対応して、縦軸\(F=0,-K(x_1-x_c),-K(x_2-x_c)\)と打ってある。
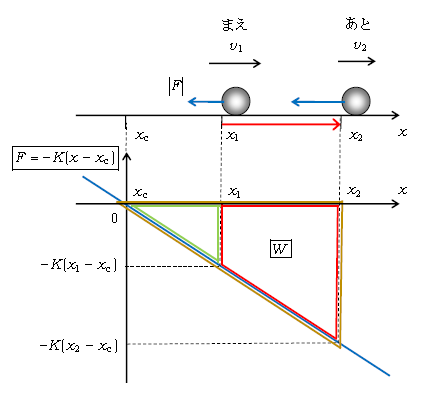
さて、仕事\(W=\) (赤い台形の面積)×(-1) [ (-1)倍したのは、力\(F\)の向き(青矢印、左向き)と移動の向き(赤矢印、右向き)が逆向きなので仕事\(W<0\)となる(1-16-1)からである ]
\(=\) { (黄色の三角形の面積)\(-\)(緑の三角形の面積) }×(-1)
\(=\) { \(\displaystyle (x_2-x_c)×K(x_2-x_c)×\frac{1}{2} \)
\(\displaystyle -(x_1-x_c)×K(x_1-x_c)×\frac{1}{2}\) }×(-1)
\(\displaystyle = \frac{K}{2}(x_1-x_c)^2-\frac{K}{2}(x_2-x_c)^2\)
これは合力\(F=-K(x-x_c)\)の仕事であるから、弾性力や重力や浮力など、ともかく全ての力の仕事をひっくるめて\(W= \frac{K}{2}(x_1-x_c)^2-\frac{K}{2}(x_2-x_c)^2\) になるという意味である。
この仕事\(W\)が運動エネルギー変化 \(\displaystyle \frac{m}{2} {v_2}^2 -\frac{m}{2} {v_1}^2 \) に等しいから
\(\displaystyle \frac{m}{2} {v_2}^2 -\frac{m}{2} {v_1}^2=W= \frac{K}{2}(x_1-x_c)^2-\frac{K}{2}(x_2-x_c)^2 \)
\(\displaystyle\) ∴ \(\displaystyle \frac{m}{2} {v_2}^2+\frac{K}{2}(x_2-x_c)^2= \frac{m}{2} {v_1}^2+\frac{K}{2}(x_1-x_c)^2 \)
\(\displaystyle\)左辺と右辺が等しいということは、
\(\displaystyle \frac{m}{2} v^2+\frac{K}{2}(x-x_c)^2=\)一定
であることを意味する。これがポイントに記したエネルギー保存則である。
つまり、合力\(F=-K(x-x_c)\)に対応して、たとえ\(K\)がばね定数でなくとも、あたかも弾性エネルギーであるかのように\(\frac{K}{2}(x-x_c)^2\)と書けば、正しいエネルギー保存則になるということなのだ。今後は\(\frac{K}{2}(x-x_c)^2\)を「形式上の弾性エネルギー」と呼ぶことにしたい。


