6-04-1: 波動性と粒子性
素粒子の全てが波動性・粒子性の二重性を持っています。
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント
・ 光子に関するアインシュタインの関係式 \(E=h\nu \) 、\(\displaystyle p=\frac{h}{\lambda } \)
電子に関するドブロイの関係式 \(\displaystyle \lambda=\frac{h}{p}=\frac{h}{mv} \) 、\(\displaystyle \nu=\frac{h}{E} \)
まずは「原子物理」を歴史の中で位置付けてみよう。
19世紀までの力学・電磁気学・ 熱力学などで構成されていた物理を「古典物理学」という。これに対して「現代物理学」は今まさに現在進行中の物理で、実験的に立証されている2本柱は、相対性理論(アインシュタイン 1905年特殊相対論、1915年一般相対論)および量子力学(ハイゼンベルク 1925年行列力学、シュレーディンガー 1926年波動力学、等々)(相対性理論と量子力学の両方を取り込んだ発展形は量子場の理論という)である。「原子物理」は古典物理学から現代物理学への過渡期の物理で、6-01-1で述べた通り「20世紀初めの数々のノーベル物理学賞で紡がれる物語」である。
古典物理学における物理的実体は2つ、「波動」および「粒子」。
たとえば光あるいは電磁波(可視光線, 紫外線, X線,\(\gamma\)線など)は波動に分類され、重ね合わせの原理に従って干渉性を示す。一方、小球は「粒子」であり、2球は衝突を起こしこそすれ、重ね合わせの原理によって干渉したりはしない。
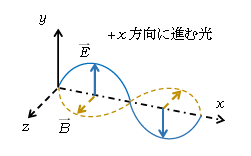
ところが、である。光を古典的な波動と捉えると光電効果を説明することはできないことに、19世紀末の物理学者は気付かされる。以下にその1つの例を説明していくと ―― 波の強度は振幅の2乗に比例する(これはひもを伝わる波については証明できるが、音波や光波では大学レベルの話になるので、そのまま受け入れてもらいたい)。光波を図示すると図1のようになる。光波では、波動の変位に当たる量が実は電場ベクトル\(\vec{E}\)(及び磁束密度ベクトル\(\vec{B}\))である(高校物理ではそういう事実がある、と理解すればよく、詳しい話は大学に任せよう)。ここで入射光の強度を強くすれば、今述べた通り強度は振幅の2乗に比例だから光に伴う電場\(E\)が大きくなり、物質中の電子に及ぼす電気力\(F=qE\)が大きくなる。すると限界振動数以下の入射光であっても電子は飛び出してくる (光電効果は起こる)はずである。しかし実験事実はそうなっていないのが19世紀末の大きな謎だった。光を「光子という粒子の集団」と捉えて光電効果を見事に解明したのがアインシュタインであることは、すでに6-02-1で述べた。
さて、古典物理学では波動と見なされていた光も、粒子と見なされていた電子も、現代物理学では二重性を持つ物理的実体と考えられている。簡単に言ってしまえば、波動性・粒子性の一方だけで捉えきることはできない実体、波動性・粒子性の両方が統合された実体だ。 (☆)
6-01-1の光子に関する関係式\(E=h\nu \)、\(\displaystyle p=\frac{h}{\lambda } \) は、 (1)
光を粒子(光子)と捉えたときの物理量であるエネルギー\(E\)、運動量\(p\)(左辺)と、
波動と捉えたときの物理量である振動数\(\nu \)、波長\(\lambda \)(右辺)を
つなぐ関係式であると見ることができる。
一方、電子に関しては「ドブロイの関係式」\(\displaystyle \lambda=\frac{h}{p} =\frac{h}{mv}\)、\(\displaystyle \nu=\frac{h}{E} \) がある。 (2)
これは電子を波動と捉えたときの波長\(\lambda \)(とくにドブロイ波長という)、振動数\(\nu \)(左辺)と、
粒子と捉えたときの運動量\(p=mv\)、エネルギー\(E\)(右辺)を
つなぐ関係式である。(1)と(2)は数学的に同値だから、既に(1)に慣れ親しんでいる者にとって(2)を覚えるのは容易だろう。
光の粒子性の例を扱ったのが6-02-1,6-02-2や6-03-1である。次の6-05-1では電子の波動性の例を取り上げよう。
現代物理学では、古典的な意味での波動・粒子全て(巨視的な天体・建造物・生物やそれらを構成する微視的な原子・分子全て)が素粒子から構成されていると考えられていて、素粒子の全てが二重性を持つ実体である。 なお、 (☆) の波動性・粒子性の統合を心底理解するためには、量子力学(大学にてしかるべき者は習える。様々な数学 ―― フーリエ変換、非可換演算子、行列力学、ヒルベルト空間における正規直交展開、群論における規約表現、等々 ―― を習得する必要あり)を学ばねばならない。ゆえに大学入試で波動性・粒子性の統合の深い理解を問われることは決してない。ご心配なく。


