6-03-1: コンプトン効果
コンプトン効果は特に立式と計算が重要です。
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント
・ コンプトン効果とは、光子と電子の弾性衝突。
エネルギー保存則と運動量保存則の\(x\)成分、\(y\)成分が成り立つ。
光子の振動数\(\nu\)、波長\(\lambda \)として、
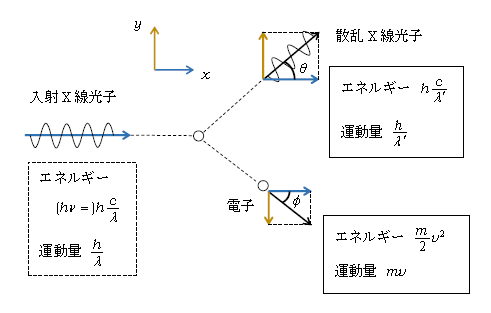
光子のエネルギーは\(\displaystyle h\nu=h\frac{c}{\lambda} \)、運動量は\(\displaystyle \frac{h}{\lambda} \) (6-01-1)。
コンプトンはX線を石墨に照射させ、石墨から飛び出してくる電子及びそれに衝突して散乱されるX線光子を調べた(図1)。
電子のことももちろん解析したとは言え、主たる関心は散乱X線であった。 (☆)
さっそく立式に取り掛かろう。弾性衝突では力学の1-19-3,1-19-2同様、以下の保存則が成り立つ(左辺が衝突前の量で図1の点線の囲み、右辺が衝突後の量で実線の囲み)。
エネルギー保存則 \(\displaystyle h\frac{c}{\lambda}=h\frac{c}{\lambda’}+\frac{m}{2}v^2 \) (1)
運動量保存則 \(x\)成分: \(\displaystyle \frac{h}{\lambda}=\frac{h}{\lambda’}\cos\theta +mv\cos\phi \) (2)
\(y\)成分: \(\displaystyle 0=\frac{h}{\lambda’}\sin\theta -mv\sin\phi \) (3)
入試では、(1)(2)(3)の保存則が正確に立てられること、さらに以下の計算をしっかりとやり切ることがコンプトン効果の2大テーマである。(☆)に述べたことから、電子にかかわる量\(\phi,v\)を消去して、散乱X線に関わる量\(\theta\)と\(\lambda’\)の関係を調べることにしよう。まず\(\phi\)を消去する。そのためには
(2)より \(\displaystyle mv\cos\phi=h\left( \frac{1}{\lambda}-\frac{1}{\lambda’}\cos\theta \right) \) (4)
(3)より \(\displaystyle mv\sin\phi=h\frac{1}{\lambda’}\sin\theta \;\:\, \) (5)
(4)\(^2+\)(5)\(^2\)で\(\phi\)を消去する(\(\cos^2\phi+\sin^2\phi =1 \)だから消去できる)。
\(\displaystyle m^2v^2=h^2\left( \frac{1}{\lambda^2}-\frac{2}{\lambda\lambda’}\cos\theta +\frac{1}{\lambda’^2}\cos^2\theta +\frac{1}{\lambda’^2}\sin^2\theta \right) \)
\(\displaystyle =h^2\left( \frac{1}{\lambda^2}-\frac{2}{\lambda\lambda’}\cos\theta +\frac{1}{\lambda’^2} \right) \) [ \(\cos^2\theta+\sin^2\theta =1 \)を用いた ]
両辺\(2m\)で割って \(\displaystyle \frac{m}{2}v^2=\frac{h^2}{2m}\left( \frac{1}{\lambda^2} +\frac{1}{\lambda’^2} -\frac{2}{\lambda\lambda’}\cos\theta \right) \)
左辺に(1)の\(\frac{m}{2}v^2 \)を代入すれば、今度は\(v\)が消去できる。
\(\displaystyle hc\left( \frac{1}{\lambda}-\frac{1}{\lambda’} \right)=\frac{h^2}{2m} \left(\frac{1}{\lambda^2}+\frac{1}{\lambda’^2}-\frac{2}{\lambda\lambda’}\cos\theta \right) \)
両辺\(hc\)で割って、さらに\(\lambda \lambda’ \)倍すると
\(\displaystyle \lambda’-\lambda=\frac{h}{2mc} \left( \frac{\lambda’}{\lambda}+\frac{\lambda}{\lambda’}-2\cos\theta \right) \)
ここでコンプトンの実験状況では\(\lambda’ \)は\(\lambda \)より数パーセント大きい程度だから、\(\displaystyle \frac{\lambda’}{\lambda} \)は1より数%大きい量(たとえば1.03)、\(\displaystyle \frac{\lambda}{\lambda’} \)は1より数%小さい量(たとえば\(\displaystyle \frac{1}{1.03}≒0.97\))あると近似すれば、\(\displaystyle \frac{\lambda’}{\lambda}+\frac{\lambda}{\lambda’} ≒2 \)となる。よって
\(\displaystyle \lambda’-\lambda=\frac{h}{mc}(1-\cos\theta) \)
が得られる。これを「コンプトン散乱の式」(1923年)といい、散乱角\(\theta\)の関数として、散乱X線の\(\lambda’\)と入射X線の\(\lambda\)の差を表したものである。コンプトンはこれにより、ノーベル賞を後に受賞した。


