1-09-1: 摩擦力（及び垂直抗力）

摩擦の３種類ーー静止摩擦、最大摩擦、動摩擦ーーをしっかり押さえましょう！　→　＜例題＞は1-09-2、1-09-3へ　　　　　　　　　　　　　　

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

ポイント　　　1-07-1と同様に「力の規則」を示す

	何から働く	向き	大きさ
垂直抗力	相手の面から	面と垂直 物体を押し返す向き	とりあえず \(N\)とおく
摩擦力	相手の面から	面と平行 すべるのを妨げる向き	３種類 図２ごと覚えよ

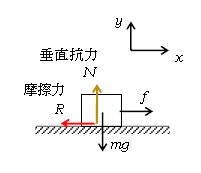
　水平な床の上の物体を手の力\(f\)で動かそうとする状況を考える（図１）。さっそく1-08-1: 力学攻略の基本　を用いる。
　まず軸と力を図示する。重力\(mg\)を書いてから、ふれているものを探すと、手と床面が物体にふれている。面から働く力は２つ ―― 面に垂直な垂直抗力と面に平行な摩擦力だ。垂直抗力は上の表の通り。

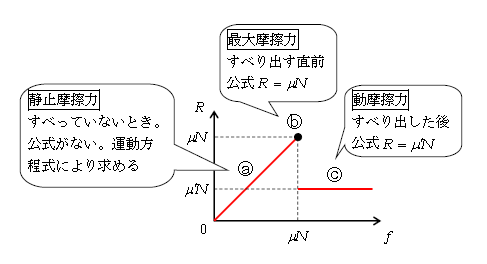
　摩擦力は上の表にプラスして、図２のグラフも理解しておこう。横軸は物体を動かそうとする力\(f\)、縦軸は摩擦力\(R\) 。
　我々が日常経験するように、\(f\)(図１)を0,0.1,0.2N,…と少し加えた位では、物体はすべり出さない。なぜなら\(R\)も0,0.1,0.2N,…と大きくなっていき、\(f\)と\(R\)がつり合ったままだからだ。物体がすべっていないときの\(R\)を静止摩擦力という。静止摩擦力\(R\)と\(f\)は等しいから、図２のグラフは傾き角45°のⓐのようになる。
　しかし\(f\)をどんどん大きくしていくと、やがて物体は今にもすべり出しそうなる。すべり出す直前の\(R\)を最大(静止)摩擦力という（ⓑ ●）。
　さらにこのときの\(f\)よりわずかでも\(f\)を大きくすると、とたんに物体はすべり出す。すべり出した後の\(R\)を動摩擦力という。動摩擦力\(R\)は一定と考えてよい（©）。

　最大摩擦力には公式がある。\(R=\mu N\)で、\(\mu \)を静止摩擦係数という（ⓑ）。\(\mu \)は例えば0.7といった単なる数である。
　動摩擦力には公式がある。\(R=\mu 'N\)で、\(\mu '\)を動摩擦係数という（©）。\(\mu’ \)も例えば0.3のような数。
　しかし静止摩擦力には公式がない（ⓐ）。すべっていないときの摩擦だから、\(x\)方向の運動方程式\(ma=m0=f-R\)（つり合いの式）を利用して\(R=f\)と求めることはできるが、すべり出す直前でしか成り立たない公式\(R=\mu N\)を決して用いてはいけない。まだ余裕ですべっていないときには公式がない、運動方程式で求めるしかないのだ。
[　なお、公式\(R=\mu N\)や\(R=\mu 'N\)は近似として（厳密に=ではなく≒の意味で）成り立っている公式で、その正当性を説明するには ―― 例えば物体と床面の接触面を少なくとも顕微鏡レベルで拡大し、物体と床面がどのように力を及ぼし合っているのかを細かく見ないといけない。それは研究者レベルの内容で、高校物理をはるかに超えている。よって入試では、理由抜きで\(R=\mu N\)、\(R=\mu 'N\)を用いてよい。 ]