1-09-3: 摩擦力 <例題2>
引き続きもう1題、摩擦を徹底的に攻略しましょう!
例題2
図のように、なめらかな水平面上に質量\(m\)の物体A、水平面に対して角度\(\theta\)傾いた斜面上に同じ質量\(m\)の物体Bがあり、A、Bはひもとなめらかかな滑車を通して連結されている。Bと斜面の間の動摩擦係数\(\mu \)、重力加速度の大きさを\(g\)とし、ひもと滑車の質量は無視する。また、水平面も斜面も十分に長いものとする。
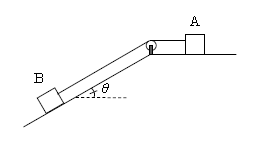
問1 はじめ、Aを手で支えておき、ついでAに右向きに大きさ\(F\)の力を短い時間加えて手を離したところ、Aは右向きにすべっていた。このときのひもの張力の大きさを\(T\)とし、Aの加速度を、右向きを正の向きとして\(a\)とする。Aの運動方程式として正しいものを、次の①~⑦のうちから一つ選べ。
① \(ma=F\) ② \(ma=-T\) ③ \(ma=-\mu mg\)
④ \(ma=F-T\) ⑤ \(ma=-T-\mu mg\) ⑥ \(ma=F-\mu mg\)
⑦ \(ma=F-T-\mu mg\)
問2 Aはしばらくすると静止し、直ちに左向きにすべり始めた。Aが左向きにすべり始めてから距離\(l\)すべるのにかかる時間はいくらか。正しいものを、次の①~⑥のうちから一つ選べ。ただし、この間AもBも滑車には衝突しなかったものとする。
① \(\displaystyle \sqrt \frac{l}{g(\sin\theta +\mu \cos\theta)} \) ② \(\displaystyle \sqrt \frac{l}{g(\sin\theta -\mu \cos\theta)} \)
③ \(\displaystyle \sqrt \frac{2l}{g(\sin\theta +\mu \cos\theta)} \) ④ \(\displaystyle \sqrt \frac{2l}{g(\sin\theta -\mu \cos\theta)} \)
⑤ 2\(\displaystyle \sqrt \frac{l}{g(\sin\theta +\mu \cos\theta)} \) ⑥ 2\(\displaystyle \sqrt \frac{l}
{g(\sin\theta -\mu \cos\theta)} \)
解答・解説
1-08-1: 力学攻略の基本 の流れに従って行く。
問1 まず軸と力 注目物体をAにする。簡単のため、水平方向の力だけを図1に示す。
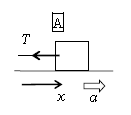
問題文1行目に「なめらかな水平面」とあるが、「なめらか」とは摩擦を考えなくてよいという意味なので、Aに加わる摩擦はない。
重要なのは、問1の問題文の「大きさ\(F\)の力を加えて手を離した」という箇所。手を離した後の運動方程式を立てるので、手を離した後は加わらない\(F\)を図に書いてはいけない。
次に\(ma=F\) \(ma=-T\) 答 ②
・ ただし、\(\displaystyle a=-\frac{T}{m} \)とやっても、張力\(T\)はとりあえず\(T\)とおいただけの未知数だから、\(a\)は求まったことにはならない。\(a\)を求めたかったら、Bの運動方程式も立ててもう1つ式を作らないといけない。したがって問2では、A、B両方を注目物体として扱う。
問2 まず軸と力 Aは左向きにすべっているから、左向きに\(x_A\)軸(図2右)。Bはすべり下りているから、斜面平行下向きに\(x_B\)軸、垂直に\(y_B\)軸(図2左)。
Aに働く力は、水平方向だけを示すと図2右の通り。Bに働く力は\(mg\)、ひもから\(T\)、斜面から「面に垂直な垂直抗力\(N\)と面に平行な摩擦力\(R\)」。摩擦力の向きは1-09-1の表の通り、すべるのを妨げる向きだから、すべり下りるのを妨げる斜面平行上向き。
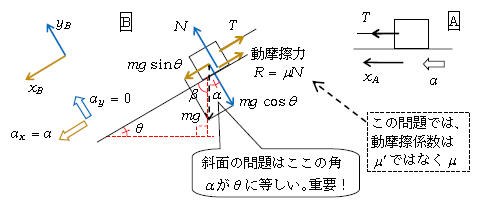
直角以外の2角の和は90°だから、\(\beta +\theta =90° \) つまり\(\beta =90°- \theta \)。
また\(\alpha +\beta =90° \)だから \(\alpha =90°-\beta=90°-(90°- \theta)=\theta \)
次に\(ma=F\) Aは左向きに\(a\)(図2右)、Bは\(a_x=a\)、\(a_y=0\)(図2左)と図示する。\(x_B\)、\(y_B\)軸に対して斜めの力\(mg\)を分解(1-08-1)。このとき図2B中に示した角\(\alpha =\theta \)であることに注意する。(その証明は図2のキャプション(説明文)を参照のこと。証明を一度理解したら、\(\alpha =\theta \)は頻出中の頻出だから覚えてしまおう。) なお、問1の\(a,T\)と問2の\(a,T\)は値が等しいとは限らないので、念のため。
図2を見ながら
Aの運動方程式 \(ma=T \; \) (1)
Bの運動方程式 \(x_B\)方向: \(ma=mg\sin\theta -\mu N-T \) (2)
\(y_B\)方向:\(m0=N-mg\cos\theta \) (3)
(1) ~(3)は\(a,T,N\)を未知数とする連立方程式。これらから\(T,N\)を消去して\(a\)を求め、あとは 運動\(v,x\)を調べる と行けばよい。
(3)より \(N=mg\cos\theta \) (2)に代入して\(N\)を消去
\(ma=mg\sin\theta -\mu mg\cos\theta -T \; \) (4)
(1)+(4)で\(T\)を消去 \(2ma=mg\sin\theta -\mu mg\cos\theta \)
∴ \(\displaystyle a=\frac{1}{2} g(\sin\theta -\mu \cos\theta) \) (5)
運動\(v,x\)を調べる 初期条件\(v_0,x_0\)に注意。Aが左向きにすべり始めたときを\(t=0\)にし、そこを原点に取ると、\(v_0=0\)、\(x_0=0\)。
\(l\)すべる時間を\(t\)とすれば、等加速度の公式より
\(\displaystyle x=l=x_0+v_0t+\frac{1}{2}at^2=\frac{1}{2}at^2 \)
\(\displaystyle ∴ t=\sqrt \frac{2l}{a} \) (5)を代入して \(\displaystyle t=2\sqrt \frac{l}
{g(\sin\theta -\mu \cos\theta)} \)
答 ⑥


