1-23-1: 単振動のxとt、vとtの関係式
1-22-1単振動の方程式 に引き続いて、単振動の時刻tでのふるまいを扱います。1-24-1単振動の時間変化の調べ方 ー 力学攻略の基本 第3弾 も是非合わせて学習しましょう。!
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント
・ 単振動は等速円運動の正射影
・ 単振動の位置\(x\)、速度\(v\)と時刻\(t\)の間には次の関係がある。
\(x=A\sin(\omega t+\phi)+x_c \)
\(v=A\omega \cos(\omega t+\phi) \)
ここで\(A\)を振幅、\(\omega\)を角振動数、\(\phi\)を初期位相といい、\(x_c\)はつり合いの位置かつ(振動)中心である。
・ 周期
\(\displaystyle T=\frac{2\pi}{\omega} \)
話を2部構成で進めていこう。
1⃣ 単振動は等速円運動の正射影であることを示す。その意味は、等速円運動している物体の\(x\)座標の動きを追うと、それが単振動と一致するということである。等速円運動している物体に(図1)\(x\)軸と垂直に(真上から)光を当ててやり、\(x\)軸上のスクリーンに写る物体の影の動きを追うと、影(\(x\)座標)は右左へ行ったり来たりの往復運動 ―― 単振動 ―― をする、それをこれから導出する。
図1に等速円運動する物体の速度\(u\)(接線方向)、加速度\(\alpha\)(中心方向)が示してある。1-19-1でやった通り、半径を\(A\)として
\(u=A\omega\) 、 \(\alpha=A\omega^2 \) (1)
\(t=0\)での中心角を\(\phi\)とし、角速度(1sあたり回る角度)を\(\omega\)とすると時間\(t\)後には\(\omega t\)回っている。\(\theta=\omega t+\phi \)とおいた角が赤い2本の弧で、合計4ヶ所書かれている。
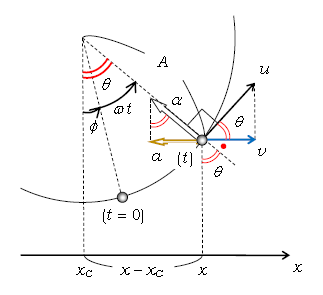
\(\theta +\)●=90°に注意
さて、図1のように円の中心の座標を\(x_c\)に取ると \(x-x_c=A\sin \theta \) (2)
速度の\(x\)成分\(v=u\cos \theta=A\omega \cos \theta \) [ (1)を用いた ] (3)
加速度の\(x\)成分\(a=-\alpha\sin \theta=-A\omega^2 \sin \theta =-\omega^2 A\sin \theta\) [ 右向きを正にしているので\(a<0\) ]
ここで(2)を用いると \(a=-\omega^2 (x-x_c) \) (4)
この(4)は等速円運動している物体の\(x\)座標の動き(影の動き)が満たしている関係式である。
ところが、1-22-1でやった通り、単振動する物体の\(x\)座標の動きは
単振動の方程式 \(a=-\omega^2 (x-x_c) \)
を満たし、(4)と完全に一致している。よって、単振動は等速円運動の影の動きと一致することが言えた。
図1より\(\theta=\omega t+\phi \)だから、結局
(2)より 単振動の\(x=A\sin (\omega t+\phi) +x_c \)
(3)より \(v=A\omega \cos (\omega t+\phi) \) となる。
なお、\(x\)の式はしっかり頭の中に入れておくとして、\(v\)の式はちょっとした微分計算で出せる。というのも、1-01-1でやった通り、\(\displaystyle v=\frac{dx}{dt}\)であるから、
\(x=A\sin \theta +x_c \) かつ \(\theta=\omega t+\phi \) に注意して
\(\displaystyle v=\frac{dx}{dt}=\frac{dx}{d\theta} \frac{d\theta}{dt} \) [ つまり合成関数の微分を用いる ]
\(\displaystyle =\frac{d}{d\theta}(A\sin \theta +x_c) \frac{d}{dt}(\omega t+\phi ) \)
\(=(A\cos \theta)\omega \) [ 定数\(x_c \) 、\(\phi\)の微分は0 ] \(=A\omega \cos (\omega t+\phi) \)
この計算は慣れれば頭の中で即座にできるようになるはず。すると、\(v\)の式は覚えなくてもよくなる。
2⃣ 基本用語を押さえる
図2は\(x=A\sin \theta +x_c=A\sin (\omega t+\phi) +x_c \)のグラフの一例で、\(-1≦\sin≦1\)により\(-A+x_c ≦x≦A+x_c\)であると縦軸に書かれている。また、左回りに等速円運動する物体に、左から光(横方向の黄色矢印)を当てたときに\(x\)軸上に写る影の動きの様子(縦方向の黄色矢印)も示してある。つまり、円運動上の〇、△、□の影がグラフ上の〇、△、□に対応していく。
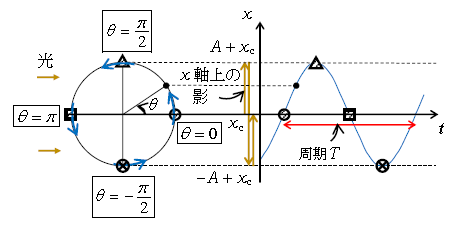
\(x_c \)は1-22-1の時点では、つり合いの位置という意味しかなかったが、グラフの縦軸から明らかなように振動範囲\(-A+x_c ≦x≦A+x_c\)の中点で、振動中心(あるいは単に中心)という。
中心\(x_c \)から最高点(あるいは最低点)までの距離\(A\)を振幅という。
\(\sin\)の中身\(\theta\)を位相という。
\(\theta=\frac{\pi}{2} \) なら \(x=A\sin \frac{\pi}{2} +x_c=A+x_c \) 最高点を通過中(図2の円およびグラフの△印を見るとよい。以下同様)
\(\theta=-\frac{\pi}{2} \) なら \(x=A\sin(-\frac{\pi}{2}) +x_c=-A+x_c \) 最低点を通過中
\(\theta=0\) なら \(x=x_c \) 中心を上向きに通過中
\(\theta=\pi\) なら \(x=x_c \) 中心を下向きに通過中
このように、位相は振動が今どのような状態にあるかを表している。
特に\(t=0\)での\(\theta=\omega t+\phi=\omega 0+\phi\)つまり\(\phi \)を初期位相という。初期位相は振動がどのような状態から始まるかを表している。
\(\omega\)(ギリシャ文字のオメガ。アルファベットのwではない。念のため)は円運動に対しては角速度というが、単振動に対しては角振動数という。\(t\)での\(\theta=\omega t+\phi\) に対して、\(t+1\text{s}\)での\(\theta’=\omega (t+1\text{s})+\phi =\omega t+\phi +\omega = \theta+\omega \) のように、\(\theta’\)は\(\theta\)よりも\(\omega\)増えている。つまり1sあたりに\(\theta\)が\(\omega\)増えているから、角振動数\(\omega\)とは1sあたりの位相\(\theta\)の増加分である。
\(\sin \theta\)は\(\sin\)の中身\(\theta\)が\(2\pi\)増えると元の値に戻る。元に戻るまでの時間を周期\(T\)という(図2のグラフの横軸)。
ということは、1sあたりの\(\theta\)の増加分\(\omega\)に、周期\(T\)をかけたものが、\(2\pi\)に等しい。
\(\omega ×T=2\pi \) ∴ \(\displaystyle T=\frac{2\pi}{\omega} \)
なお、単振動は等速円運動の正射影だから、単振動の周期\(T\)が1-19-1の等速円運動の周期公式 \(T=\frac{2\pi}{\omega} \) と一致するのは当然である。
→ 単振動の時間変化の調べ方 ー 力学攻略の基本 第3弾 は1-24-1へ


