1-03-1: 等加速度直線運動

等加速度直線運動の公式は便利だから、覚えて、自在に使いこなせるようにしておきましょう！　　　　　　　

※　ページ最上部の（一部スマホでは右上または下側の $\equiv$ 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

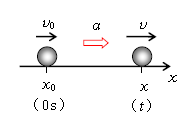
　図１で０sでの速度を初速度$v_0$、位置を初期位置$x_0$といい、$v_0$と$x_0$をまとめて初期条件という。どんな運動でも、初期条件をしっかり押さえることはとても大切だ。

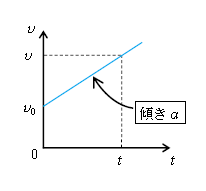
　単元タイトルの等加速度直線運動とは、その名の通り、加速度が一定のままの運動。加速度$a=v$-$t$グラフの傾きだから、傾きが一定値$a$の図２のような$v$-$t$グラフになる。縦軸の速度$v$が一定の割合で増えつつ加速していく様子を表したグラフだ。

　ポイントにまとめた等加速度の公式(1)、(2)の証明をしよう。
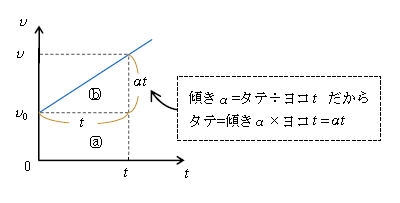
(1)： 図３の四角の囲みに注意しつつ縦軸を見ると、$v=v_0$加えることの$at$、つまり(1)式がすぐ証明される。
(2)： $v$-$t$グラフの面積＝変位（1-02-1）だから、
　　　図１の変位$x-x_0$＝図３の(ⓐの面積)+(ⓑの面積)=$v_0t+t×at÷2$
　　　∴　$\displaystyle x=x_0+v_0t+\frac{1}{2}at^2$　よって証明された。

　この公式(2)は、速度が一定のままの「等速」直線運動と比較すると覚えやすい（図４）。

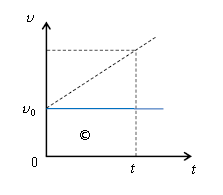
　「等速」の場合は、変位$x-x_0$＝図４の©の面積＝$v_0t$　これは要は[m]=速度×時間 という意味。
　　∴　$x=x_0+v_0t$　　　　　　　　(3)　　　　　　　　　　　　　　　　　　　　　　　　　　
　(3)式「等速」と比べて、(2)式「等加速度」の方が右辺が$\frac{1}{2}at^2$だけ多いのは、加速している分だけ変位が多い、と理解すればよい。しかも、多い分は図３の三角形ⓑの面積だから、底辺×高さ÷２の $\frac{1}{2}$が付く公式というわけである。