3-19-1: ジュール熱
抵抗で発生する熱「ジュール熱」は回路のエネルギー式にとって重要です!
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント
・ オームの法則 \(\displaystyle I=\frac{V}{R} \) または \(V=RI\) (\(R\) [Ω] は(電気)抵抗)
・ 単位時間当たりのジュール熱(抵抗の消費電力)\(P\) [W] \(\displaystyle =IV=RI^2=\frac{V^2}{R}\)
導体に加わる電圧\(V\) [V] と流れる電流\(I\) [A] との間には次のオームの法則が成り立つ。
\(\displaystyle I=\frac{V}{R} \) または \(V=RI\) (1)
ここで\(R\)を(電気)抵抗という。同じ電圧\(V\)に対しては\(R\)が大きいほど\(I\)は小さいことから、\(R\)は「電流の流しにくさ」を表す量である。\(R\)の単位は[Ω](オーム)といい、(1)より[Ω=V/A]。(電気)抵抗という用語は「(電気)抵抗\(R\)を備えたニクロム線などの回路素子(電気回路中の部品)」という意味でも用いられる。抵抗値は斜体の\(R\)で表すが、回路素子の名前としては立体文字のRを用いて、「抵抗値\(R=\)700Ωの抵抗R」と表現したりする。
抵抗に電流を加えると熱が発生し、それを特にジュール熱という(電気ストーブがその良い例)。図1のような電池(起電力\(V_0\))、導線、抵抗(抵抗値\(R\)、回路記号は長方形)からなる回路を考えよう。点Aからスタートして、点Bを経て、再び点Aに戻るときの電位の上がり下がりの様子を示したのが図2。
図1で右向きに抵抗をたどるのが図2(a)。抵抗では電流の向きに電位が下がる。抵抗を流れる電流はちょうど高い所から低い所へ流れる水のようである。電圧降下(電位の下がり分)は(1)の\(V=RI\)。
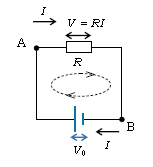
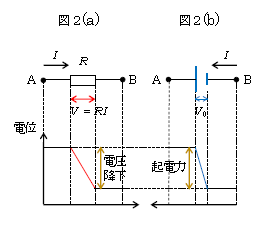
図1で左向きに電池をたどるのが図2(b)。3-09-2でやった通り、電池は負極から正極へ電位を汲み上げるポンプの役目をしているから、電池を負極から正極へ流れる電流の向きにはむしろ電位が上がる。起電力(電位の上がり分)は\(V_0\)。
[ ところで、導線部分が等電位である(電位の上がり下がりはない)ことの理由として、3-13-1では「導線はひとつながりの導体を成す」からであると述べた。ではなぜ「ひとつながりの導体は等電位」なのかは、3-06-1「静電誘導」に説明がある。しかし、この説明を注意深く読むと、等電位になるのはあくまでも「帯電完了後(すなわち自由電子の移動が止まった後)」。自由電子が移動している間、つまり電流が流れている間は、導体は等電位である必要はない。実際、この単元のここまでの記述で分かる通り、導体の電位は電流の向きに\(V=RI\)だけ下がる。ところが、である。導線に広く用いられている素材の銅の抵抗値は非常に小さいので、電気抵抗という長方形の回路記号で表される部分の抵抗値に比べて無視できる。というわけで、電流が流れている導線部分も等電位であるとして扱ってよい。 ]
さて、キルヒホッフ(の第2法)則(3-13-1)により 電圧降下 \(RI=V_0\) 起電力 (2)
いま両辺に、微小時間\(\Delta t\)に流れる電荷\(\Delta q=I\Delta t\)(3-01-1)を掛け算してみよう。というのも、(2)の両辺の単位は[V=J/C]、\(\Delta q\)の単位は[C]だから、それらの掛け算の単位は[J/C×C=J]。つまり、キルヒホッフ則×\(\Delta q=I\Delta t\)で、エネルギーのことが調べられるはずである。
(2)の右辺×\(\Delta q=\Delta q \cdot V_0\) (3)
これは3-09-2より、電池のする仕事に他ならない。一方、左辺には\(\Delta q=I\Delta t\)の\(I\Delta t\)の方を掛けて、
(2)の左辺×\(I\Delta t=RI^2\Delta t\; \) (4)
(4)=(3)より \(RI^2\Delta t=\Delta q\cdot V_0\; \) (5)
3-13-1の通り、起電力には「電位(1Cあたりの位置エネルギー)の上がり分」、すなわち1Cあたりのエネルギーの上昇分という意味がある。ゆえに、(3)はまさに電池のする仕事の分のエネルギーの上昇を指す。
一方、電圧降下は「電位の下がり分」、すなわち1Cあたりのエネルギーの下降分という意味がある。ゆえに、(4)は抵抗で失われる\(\Delta t\)間のジュール熱と見なせる。
結局(5)は、抵抗で発生する熱量=電池のする仕事 というエネルギー保存を表す。
ここで、(4)より単位時間当たりのジュール熱\(P=RI^2\)。次々に式変形していくと、
\(\displaystyle P=I×RI=IV=\frac{V}{R}V=\frac{V^2}{R}\) 。公式としてまとめると
単位時間当たりのジュール熱\(\displaystyle P=IV=RI^2=\frac{V^2}{R}\)(ジュールの法則)
\(P\)の単位は[J/s=W](ワット)。\(P\)を抵抗の消費電力ともいう。


