1-12-1: 浮力
浮力は水圧による合力によって生じることを、きっちり理解しましょう! → <例題>は1-12-2へ
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント 1-07-1と同様に「力の規則」を示す
| 何から働く | 向き | 大きさ | |
| 浮力 | 周りの液体・ 気体から | 鉛直 上向き | 押しのけられた液体・気体に かかる重力の大きさ |
・ 特に、液体から加わる浮力の大きさは\(F=\rho _水 V_下 g \)
\(\rho _水 \): 液体の密度[\(\text{kg} \)/m\(^3\)]
\(V_下 \): 物体の体積のうち液面より下の部分[m\(^3\)]
※ 1-11-1でやった水圧の公式を載せておく。
水圧\(P=P_0+\rho gh \) (1)
\(P_0\): 大気圧、\(h\): 深さ(水面からの距離)
1-11-1に引き続き、ここでも静水を扱おう。
水中の物体には周りの水から水圧が加わる。(1)より深いところほど水圧は大きいから、図1で物体の上面に加わる水圧\(P_1\)よりも下面に加わる水圧\(P_2\)の方が大きく、合力\(F\)は上を向く。これが浮力だ。
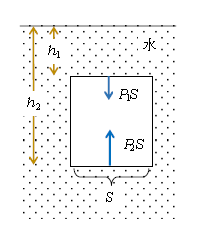
浮力\(F=\)水圧による力の合力 (2)
\(=P_2 S -P_1 S \)
(1)を用いれば、
\(F=(P_0+\rho gh_2)S -(P_0+\rho gh_1)S =\rho \cdot S(h_2 -h_1) \cdot g \) (3)
ここで\(S(h_2 -h_1) \)は物体の体積だが、言いかえると、「物体が存在することにより、本来そこにあったはずの水が押しのけられた分の体積」とも言える。この\(S(h_2 -h_1)=V \)とおけば、(3)より\(F=\rho Vg \)。
\(\rho V \)は押しのけられた水の質量([\(\text{kg} \)/m\(^3\) ×m\(^3\)])だから、「浮力の大きさ\(F\)は、押しのけられた水にかかる重力の大きさに等しい」(アルキメデスの原理)。
さて、なぜ物体の体積を、わざわざ「押しのけられた水の体積」と言い換えたのかといえば、もちろん理由がある。
例えば、水面に浮く物体に働く浮力を求めてみよう。
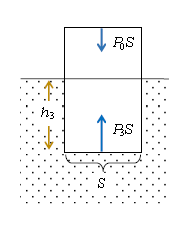
(2)より浮力\(F=P_3 S -P_0 S \)
(1)を用いれば、
\(F=(P_0+\rho gh_3)S -P_0 S =\rho \cdot Sh_3 \cdot g \)
ここで\(Sh_3\)は、物体のうち水面より下にある部分の体積だから、物体の体積とは呼べない。しかし、物体によって押しのけれた水の体積とは呼べる。浮力\(F\)に関わるのは、物体の体積ではなく、あくまでも「押しのけられた水の体積」である。\(Sh_3=V_下 \)とでもおこう(水面より下の体積という意味)。浮力公式は\(\rho Vg \)ではなく、\(\rho V_下 g\)と覚えるべきである。
ところで、この手の問題では水の密度\(\rho \)だけでなく、物体の密度(例えば\({\rho}’ \))も与えられることがよくある。もちろん浮力公式には水の密度\(\rho \)の方を用いる。
結局、浮力公式は\(F=\rho _水 V_下 g \)と覚えるのがよい。
最後に注意点を1つ ―― (2)より、浮力=水圧による合力だから、図に浮力\(F\)を書き込んだらもはや水圧による力を書き込んではいけない。水圧を二重数えすることになってしまう。
→ <例題>は1-12-2へ


