6-09-2: 崩壊の法則

この単元は直観的に理解できます！　　　　　　　　　　　　　　　　　

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

　ひじょうに多数かつ同種の原子核\(^{A}_{Z}\text{X} \)(略してX) の集団が\(\alpha\),\(\beta\),\(\gamma\)いずれかの放射性崩壊を起こしているとする。同種であるがゆえに、どの原子核Xにいつ崩壊の起こる確率も一様に確からしい（このことは、量子力学という大学の課程を用いると、厳密に証明できる）。すると、ポイントの崩壊の法則 ―― 単位時間あたりの崩壊数は、その時点の原子核Xの数に比例する ―― が成り立つことはほぼ自明だろう。つまり、原子核Xの数が例えば\(\frac{1}{3}\)に減ったなら、原子核X各々にいつ崩壊の起こる確率も等しいのだから崩壊数も\(\frac{1}{3}\)に減るというわけである。
　なお、放射能の強度とは、定義により単位時間あたりの崩壊数のことで、単位は[1/s=Bq]（ベクレルという）。6-02-2で述べた光の強度（1m\(^2\)あたりを1sあたり通過する光のエネルギー[J/(m\(^2 \cdot\)s)]）との違いに注意しよう。

　さて、ある時刻\(t\)に原子核Xの数がたとえば256×10\(^{15}\)個あったとして、半分の128×10\(^{15}\)個になるまでの時間を\(T\)とおく。原子核X各々にいつ崩壊の起こる確率も等しいのだから、次にその半分の64×10\(^{15}\)個になるまでの時間も\(T\)、そのまた半分の32×10\(^{15}\)個になるまでの時間も\(T\)、･･･となることはほぼ自明だろう。これをイメージするには ―― いま「細胞分裂ゲーム」なるゲームを制作する際、どの細胞にいつ分裂の起こる確率も等しくなるようにプログラミングをしておくなら、8×10\(^{6}\)個、16×10\(^{6}\)個、32×10\(^{6}\)個、･･･と2倍に増えていく時間が毎回毎回等しくなることは直観的に明らか。その「倍々ゲーム」をひっくり返した「半分半分ゲーム」のような状況が、原子核の崩壊であるとイメージすればよい。この\(T\)(原子核Xの数が半分になるまでの時間)を半減期という（なお、上に述べた「細胞分裂ゲーム」が面白いゲームかどうかはまた別の話）。
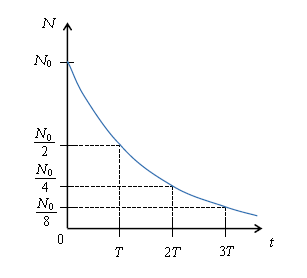
　すると、横軸の時刻\(t\)の関数として、縦軸に原子核Xの数\(N\)を取ったグラフは図１のようになる。これから時刻\(t\)での\(N\)と時刻\(t=0\)での\(N_0\)との関係が
　　\(\displaystyle N=N_0 \left( \frac{1}{2} \right)^{\frac{t}{T}} \)
となることがすぐ見て取れる。というのも、\(\displaystyle \frac{1}{2}\)の指数の\(\displaystyle \frac{t}{T}\)は、\(t=0\)から\(t\)までに半減期\(T\)(半分になるまでの時間)を何回分経過したかの数を表している。
　\(\displaystyle \frac{t}{T}=2\)なら\(t=2T\)すなわち半減期2回分だから \(\displaystyle N=N_0×\frac{1}{2}×\frac{1}{2}=N_0\left( \frac{1}{2} \right)^2 \)、
　\(\displaystyle \frac{t}{T}=3\)なら半減期3回分だから \(\displaystyle N=N_0×\frac{1}{2}×\frac{1}{2}×\frac{1}{2}=N_0\left( \frac{1}{2} \right)^3 \)、･･･というようになるわけである。