6-07-1: X線のスペクトル

連続Ｘ線と特性Ｘ線の違いをしっかり押さえましょう！　　　　　　　　　　　　　　　　　

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

　6-01-1で述べた通り、Ｘ線とは電磁波の一種で、波長\(\lambda\)=10\(^{-10}\)mを中心として、その10倍(ときには100倍)から10分の１(ときには100分の1)程度までのものを指す。X線を発生させる装置「X線管」が図１だ。
　光電管(6-02-2)と同様に、X線管も中を真空に近い状態にしたガラス管。「陰極」とあるのはタングステンのフィラメントで、図の左側にある電源を通じて電流を流すと2000Kを超す高温となり、フィラメントから電子(「熱電子」という）が放出される。図の下側に書いた高電圧\(V\)は10000V程度で、この電圧によって電子は「陽極」(金属)に向けて加速される（高電位\(V\)の陽極から低電位≒0Vの陰極に向かう左向きの電場が生じ、負電荷の電子はその電場と逆向き、すなわち右向きの電気力を受けて右向きに加速する）。なお、高電圧で陽極に達するときの電子の運動エネルギー\(K\)に比べて、陰極から放出された時点での熱電子の運動エネルギーは小さく無視できる(\(K\)≒0).

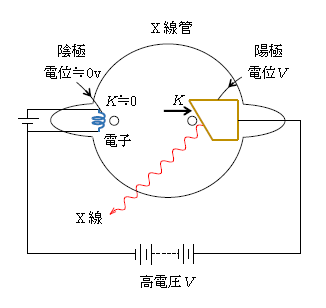
　6-01-2のエネルギー保存則　\(\displaystyle \frac{m}{2} v^2+(-e)\phi \)＝一定　を図１について立てると、
　　陽極側　　　　　陰極側
　\(K+(-e)V=0+(-e)0\text{v} \)　　∴　\(K=eV \)　

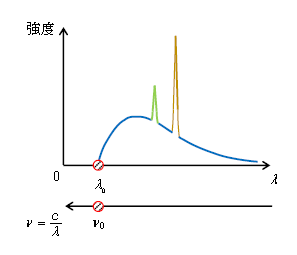
　それでは、本題のX線スペクトルの話に移ろう。ここで言うスペクトルとは、横軸の波長\(\lambda\)の関数として縦軸にX線の強度を取ったもの（図２）。横軸には振動数\(\nu\)も示してある。\(\lambda\)が小さくなって\(\lambda\)軸の左へ行くと、\(\nu=\frac{c}{\lambda}\)は大きくなるから、\(\nu\)軸の矢印は左向きに付けてある。6-02-2の通り、強度とは「1m\(^2\)あたりを1sあたり通過するエネルギー」（[J/(m\(^2 \cdot\)s)]）すなわち強度=「(1m\(^2\)あたりを1sあたり通過する光子数)×(1光子のエネルギー\(h\nu\))」。ということは、ある横軸の値\(\nu\)に対しては、発生するX線の光子数(1m\(^2\)あたり1sあたり)が多いほど縦軸の強度は大きい。
　ここで青いグラフを連続X線のスペクトル、黄色と緑のグラフを特性X線(固有X線)のスペクトルという。それらの発生メカニズムを順番に説明していく。

1⃣　連続X線（図３(a)）
　エネルギー\(K=eV\)を持つ電子を図３(a)のように陽極金属の表面に入射すると、電子が金属中で急停止したり急に軌道を曲げられたりする(その様子は図３(a)には書いてない）。このとき電子は加速度を持つ。加速度運動する電子は電磁波を発生する(6-06-1)から、X線光子が1個発生したり、10個発生したり、･･･（個数は確率論的にまちまちである）。この過程で電子は金属中の原子に力を及ぼし、原子は振動してそれが熱エネルギー\(Q\)に変換する（陽極はひじょうに高温になる）。この際のエネルギー保存則は
　\(eV=Q+h\nu+h\nu’+\cdots \)　　(☆)
熱電子は陰極から次々と多数放出されるから(図１)、陽極金属の表面に多数の電子が入射し(図３(a))、発生する光子の\(\nu\)は様々な値で分布することになり、図２のような連続的なスペクトルが得られる。
　なお、図３の(a)と(b)は入射側と発生側が逆になっている。ただし、連続X線と光電効果が「真逆」だという意味ではない（たとえば光電効果には仕事関数\(W\)が関わってくる）。連続X線と光電効果の違いを浮き彫りにする意味で(b)を挙げた。

　連続X線の特徴は最大振動数\(\nu_0\)すなわち最短波長\(\lambda_0\)を持つことである（図2の赤丸印）。これは式(☆)で、入射電子のエネルギー\(eV\)を光子1個だけが「総取りし」、熱エネルギー\(Q\)も発生しない場合。光子1個だけがエネルギー\(eV\)を総取りすれば、光子自身のエネルギー\(h\nu\)は当然最大となって\(\nu\)も最大となる。このとき(☆)より
　\(\displaystyle eV=h\nu_0=h\frac{c}{\lambda_0} \)　　　　　　　　　　 (1)
(1)は入試で頻出である。

2⃣　特性X線（図４）
　6-06-2で「水素」原子のエネルギー準位について説明したが、金属など原子一般にエネルギー準位(とびとびのエネルギー値)は存在する。電子が入射してくると（図４点線の黒丸）、陽極原子中の電子（点線の白丸）をはじき飛ばすことがある（図４①）。物質は放っておけばそのエネルギーを低くして安定化しようとするから、より高いエネルギー準位にある電子（実線の白丸）が、空席になった低いエネルギー準位に飛び移る（②）。するとボーアの振動数条件(6-06-3)に従ってX線光子が1個放出される（③）。たとえば黄色と緑のどれか1つが起こり、どれが起こるかは確率論的にまちまちである。
　振動数条件は　\(\displaystyle h\nu=h\frac{c}{\lambda}=E_n-E_l \)　　(2)
　ここで、エネルギー準位\(E_n、E_l \)は金属ごとに決まっている固有の値だから、特性X線の\(\nu、\lambda\)も金属ごとに決まっている。
　いま、入射電子の加速電圧\(V\)を大きくしてみよう。すると(1)より最大振動数\(\nu_0\)が大きくなって(最短波長\(\lambda_0\)が小さくなって)、図２の横軸上で\(\nu_0\)(\(\lambda_0\))の位置が左へとずれる。しかし、陽極金属の種類を変えない限り、特性X線（図２黄色や緑）の横軸上の位置は変わらない。

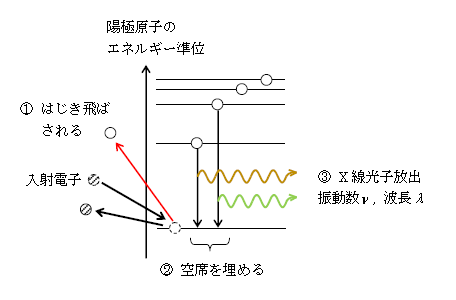
　なお、図４の黄色と緑でエネルギー準位の間隔が小さいのは黄色である。すると(2)より、黄色の方が緑よりも\(\lambda\)が大きい。図２の黄色と緑の横軸上の位置関係がまさにそうなるように色を付けてある。