6-06-1: ボーアモデル #その1
原子物理の3大分野の第2弾です。3つの単元にわたる内容ですが、しっかり頑張りましょう! → <#その2>は6-06-2、<#その3>は6-06-3へ
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント (式の説明は本文を参照のこと)
・ リュードベリの公式 \(\displaystyle \frac{1}{\lambda}=R \left( \frac{1}{l^2} – \frac{1}{n^2} \right) \)
・ 円運動の方程式 \(\displaystyle m\frac{v^2}{r} = k\frac{e^2}{r^2} \)
エネルギー保存則 \(\displaystyle E=\frac{m}{2}v^2+\left( -k\frac{e^2}{r} \right) \)
・ 量子条件 \(\displaystyle 2\pi r =\frac{h}{mv}×n \)
「19世紀末の当時不可解と思われていた様々な現象」のいま1つが「水素原子のスペクトル」である。これは水素を放電現象で高温にさせたとき、水素原子が出す光の強度と波長の関係を調べたもの。19世紀末から20世紀初めに実験データの解析が進み、1890年には既に水素原子に関する「リュードベリの公式」が提唱されている ――
\(\displaystyle \frac{1}{\lambda}=R \left( \frac{1}{l^2} – \frac{1}{n^2} \right) \)
\(\lambda \):水素原子の出す光の波長
\(R\):リュードベリ定数 =1.1×10\(^7\)1/m
\(l=1,2,3,\cdots \) ; \(n=l+1,l+2,l+3,\cdots\)
光の波長は当然光を出す水素原子の構造と密接に関連しているはずで、ではこのような発光をする水素原子の構造とはどんなものであるか、また発光はどのようなメカニズムでなされるのかが当時の物理学の大問題であった。こうした中1913年ボーアが現在「ボーアモデル」として知られている理論を提唱し、後にノーベル賞を受賞する。
ボーアモデルは様々な仮説から構成されている。たとえば「定常状態の仮説」だが、これは初読では意味がほとんど取れないという人が圧倒的だと思うので、あまり気にしないでもらいたい。とりあえず以下に記すと、
定常状態の仮説 ―― 電子のエネルギーは連続的にどんな値でも取り得るのではなく、限られたとびとびの値(離散的な値)しか取り得ない。特定の1つのエネルギーに対応した状態を「定常状態」と呼ぶ。定常状態においては電子は電磁波を放出せず、安定的に存在する。 (☆)
しばらく他の仮説の説明をしてから、またこの仮説に立ち戻ることにしよう。
では、これからボーアモデルの意味がつかみやすいように、仮説を(I),(II),(III)に大別して順次解説していく。
(I) 古典力学の仮説
水素原子は図1のように中心にある陽子の周りを電子が等速円運動する構造を持つと、ボーアは仮定した。これはラザフォードがα線の散乱実験に基づいて既に提唱していたモデルを踏襲したものである。ただしこのモデルには重大な欠点がある。円運動は向心加速度を有する加速度運動であるが、古典電磁気学によれば、加速度運動する電子は電磁波を放出し、エネルギーを失いながら中心へと落ち込んでしまう。これは原子がその「大きさ」を失って1点に潰れてしまうことを意味し、原子の安定性を説明することができない(我々の身体をつくる原子が潰れてしまうとしたなら、我々の体が潰れてしまうことになるが、そんなことは現実には起きていない)。
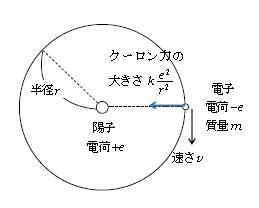
であるからこそ図1はあくまでも仮説なのであり、ボーアはさらに図1に古典力学を適用できると仮定した。
すると、第1に円運動の方程式(1-20-1)が立てられる:
\(\displaystyle ma_中=m\frac{v^2}{r} \; =F_中= \)合力の半径方向成分(中心向き正)
図1では \(\displaystyle m\frac{v^2}{r} = k\frac {e^2}{r^2} \) (1)
第2にエネルギー保存則も立てられる。電荷\(+e\)の陽子のつくる電位\(\displaystyle \phi=k\frac {e}{r}\)(3-03-1)の下、電荷\(q=-e\)の電子の持つ位置エネルギー\(\displaystyle U=q\phi=(-e)\phi=-k\frac {e^2}{r} \)であるから、
図1では エネルギー\(\displaystyle E=\frac{m}{2}v^2+ \left( -k\frac {e^2}{r} \right) \) (2)
(II) 量子条件の仮説
さて、唐突の感は否めないのだが、ボーアの次なる仮説は量子条件:
円周=ドブロイ波長×整数 (ドブロイ波長については6-04-1を参照)
\(\displaystyle 2\pi r = \frac{h}{mv}\)
× \(n \) (3)
である。(☆)の定常状態とは、実はこの量子条件を満足する状態のことである。(☆)で述べた通り、定常状態では電子は電磁波を放出せず安定的に存在するとボーアは仮定したのだ。
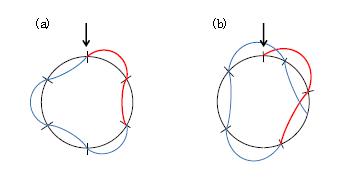
ただ、歴史的にはボーアは(3)をこれと同値な\(\displaystyle mrv=n\frac{h}{2\pi} \)という式で表していて、しかもその意味の説明を事実上棚上げにしている。時を経てボーアの理論から10年経った1923年、ドブロイによって電子の波動性が提唱されると、量子条件の意味はようやく次のように理解されるようになったというのが実状である ―― 「量子条件とはちょうど電子波の定常波が立つような条件であり、定常波の立つ状態でのみ、電子は電磁波を放出せず安定的に存在する」(図2)。
図2(a)に示したのは、赤色を付けた部分がドブロイ波長1つ分だとして、円周がピッタリ3波長分のとき。すると矢印の所で波がなめらかに接続するから、電子が円運動を何周、何千周しても波形が(a)のまま定常的である。このようなとき電子は電子は電磁波を放出せず安定的に存在する(のではないだろうか)。
一方、図2(b)は円周がドブロイ波長の整数倍でないとき。すると矢印の所で波がかみ合わず、波形が円の外側にくる部分と、円の内側にくる部分が重なり合うことになる。つまり、波の変位が互いに逆符号の重ね合わせになり、このようなときは電子は安定的に存在できない(のではないだろうか)。
ここで、(のではないだろうか)という文言を2ヶ所挿入した理由については、6-06-3中の「ボーアモデルを歴史的に振り返る」という段落で述べることにしたい。