6-06-2: ボーアモデル #その2
ボーアモデルでよく出題される計算のコツを含めて解説していきます。 → <#その1>は6-06-1、<#その3>は6-06-3へ
ポイント (式の説明は本文を参照のこと)
・ 軌道半径\(r_n \propto n^2 \)
・ エネルギー準位\(\displaystyle E_n=-|E_1|\frac{1}{n^2} \)
※ 6-06-1の式(1)-(3)を右に再掲しておく。
円運動の方程式 \(\displaystyle m\frac{v^2}{r} = k\frac{e^2}{r^2} \, \) (1)
エネルギー保存則 \(\displaystyle E=\frac{m}{2}v^2+ \left( -k\frac{e^2}{r} \right) \) (2)
量子条件 \(\displaystyle 2\pi r =\frac{h}{mv}×n \) (3)
入試では、(1)-(3)の立式が正確にできること、さらにこれらを連立して\(r\)、\(E\)を求める計算をしっかりやり切ることが、6-06-1、6-06-2までのボーアモデルに関する頻出テーマである。
・ 軌道半径\(r\): (1)、(3)より\(v\)を消去する
(3)より \(\displaystyle v=\frac{h}{2\pi rm}n \) (3′)
(1)に代入 \(\displaystyle \frac{m}{r}\frac{h^2}{4\pi^2 r^2 m^2} n^2 =k\frac{e^2}{r^2} \)
両辺の分母の\(r^2\)を約分 \(\displaystyle \frac{1}{r}\frac{h^2}{4\pi^2 m} n^2 =k e^2 \)
さらに\(r\)を数列の一般項\(r_n\)のように表して、
\(\displaystyle r_n=\frac{h^2}{4\pi^2 ke^2 m} n^2 \) \(\propto n^2 \) \((n=1,2, \cdots) \) (4)
[ 念のためだが、\(\propto\)は「比例する」という意味の記号。なお、(4)を(3′)に代入すれば \(\displaystyle v_n=\frac{2\pi ke^2}{h} \frac{1}{n}\) が求まる ]
・ エネルギー\(E\): (2)を使う前に、(1)を用いて(2)を簡単にしておくのがコツ
(1)×\(\displaystyle \frac{r}{2}\) \(\displaystyle \frac{m}{2}v^2 = \frac{1}{2}\frac {ke^2}{r} \)
\(\displaystyle\)(2)に代入 \(\displaystyle E=\frac{1}{2}\frac{ke^2}{r}-\frac {ke^2}{r} =-\frac{1}{2}\frac{ke^2}{r} \)
\(\displaystyle\)これに(4)を代入 \(\displaystyle E=-\frac{ke^2}{2} \frac{4\pi^2 ke^2 m}{h^2}\frac{1}{n^2} \)
\(E\)を一般項\(E_n\)のように表して、
\(\displaystyle E_n=-\frac{2\pi^2 k^2 e^4 m}{h^2} \frac{1}{n^2} \) \((n=1,2, \cdots) \) (5)
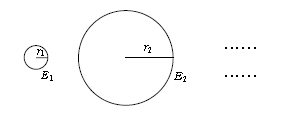
・ 電子の軌道半径\(r_n\)、エネルギー\(E_n\)は、(4)(5)から分かる通り連続的にどんな値でも取り得るのではなく、限られたとびとびの値(離散的な値)しか取り得ない。これは古典的・巨視的な粒子には見られなかった現象である(図1)。
この離散性(、不連続性、量子性とも言える)は、電子が波動性を持っているからこそ、すなわち波の数が整数に限定されたからこそ(式(3))生じている。
とくに\(\displaystyle r_1=\frac{h^2}{4\pi^2 ke^2 m} =0.53×10^{-10}\)mを「ボーア半径」といい、水素原子の典型的な大きさに対応する。
また、このタイミングでもう1回6-06-1の(☆)定常状態の仮説 を読んでおくとよい。
・ エネルギー準位\(E_n\):とびとびのエネルギー値のこと
(5)より \(\displaystyle |E_1|=\frac{2\pi^2 k^2 e^4 m}{h^2} \)
これを再び(5)に戻して \(\displaystyle E_n=-|E_1|\frac{1}{n^2} \) (5′)
と表しておくと、式が扱いやすい。
まず、エネルギー準位\(E_1,E_2,\cdots \)は負の値であるが、これには何の問題もない。エネルギーの値は基準の取り方しだいで正にも負にもなるからである(例えば重力による位置エネルギー\(mg\)×高さの基準を標高10mに取ったならば、高さ3mの所の位置エネルギーは\(mg\)×(-7m)と負の値になる)。
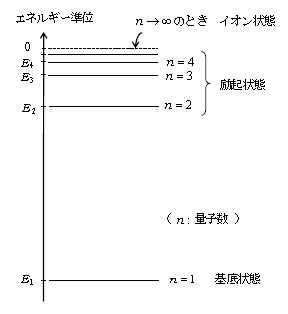
いま\(n → \infty \)とすると(5′)より\(E_n → 0 \)、すなわち\(n → \infty \)のときがエネルギーの基準である。
一方このとき(4)より\(r_n \rightarrow \infty \)、すなわち電子は陽子から完全に離れ、水素原子はイオン状態になっている。ゆえにエネルギー0となるのはイオン状態である。電子のエネルギーが負であることは、電子がイオン状態から原子中に取り込まれると、エネルギー的により低くなる(安定になる)ことを意味する。
また、(5′)より\(\displaystyle |E_2|=\frac{1}{4}|E_1|\) , \(\displaystyle |E_3|=\frac{1}{9}|E_1|\) , \(\displaystyle |E_4|=\frac{1}{16}|E_1| \) , \(\cdots \)
絶対値とは、言うまでもなく原点からの距離のことであるから、図2が得られる。
なお、\(|E_1|=21.9×10^{-19}\)J \(=13.6\)eV は水素原子の「イオン化エネルギー」に対応している。
→ <#その1>は6-06-1、<#その3>は6-06-3へ