3-02-1: 電場と電気力線
目に見えずにイメージしづらい電気現象を明快に解説していく招待状第１弾です（招待状は全部で３つ）。 → 3-03-1、3-04-1へ続く
※ ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント
・ 電場（または電界）\(\vec{E} \)=＋1Cあたりに働く力 [N/C]
・ 点電荷\(Q\)のつくる電場\(\vec{E} \)
向き \(Q\)>0のときは\(Q\)から+1Cへの斥力の向き
\(Q\)<0のときは\(Q\)から+1Cへの引力の向き
大きさ（強さともいう） \(\displaystyle E=k\frac{|Q|}{r^2} \)
\(Q\): 電気量[C]
\(r\): 電荷\(Q\)からの距離[m]
\(k\): クーロンの法則の比例定数
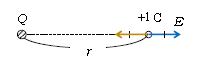
黄色の\(E\)が\(Q\)<0の場合
・ 点電荷\(q\)に働く電気力\(\vec{F}=q\vec{E} \)。負電荷\(q\)<0では力\(\vec{F}\)は\(\vec{E} \)と逆向き。
・ 電気力線の向きは\(\vec{E} \)の向き。＋から出る。ーへ入る。
この単元の電荷とは、大きさの無視できる点電荷を指す。
3-01-1で電荷どうしの間には電気力が働き、その理由は宇宙がそのようにできているから、ということを述べた。電気力の働き方をもう少し詳しく言うと次のようになる。
1⃣ 電荷\(Q\)が周りの空間を特殊な空間に変える（宇宙はそのようにできている！）
2⃣ その特殊な空間から他の電荷\(q\)が電気力を受ける（宇宙はそのようにできている）
1⃣ 電荷\(Q\)(例えば\(Q\)>0)の周りの空間の特殊性を数式で表すために、空間の各点各点に公平に+1C（単位電荷）を置いては外すことを試みると（図１）、1Cには場所ごとに様々な電気力\(\vec{F}\)が働く。例えば\(Q\)からの距離が近い所では電気力\(\vec{F}\)は強く、遠い所では弱い。電気力\(\vec{F}\)が強い場所は空間の特殊性が強いと呼ぶことにし、電気力が弱い場所は特殊性が弱いと呼ぶことにする。ここで
電場（または電界）\(\vec{E} \)=＋1Cあたりに働く力 [N/C]
と定義すれば、その強弱がまさに空間の特殊性の強弱を表している。つまり電場\(\vec{E}\)とは、数式的には1Cあたりに働く力であるが、意味的には電荷\(Q\)の周りの特殊な空間といったところである。クーロンの法則により、点電荷\(Q\)のまわりの電場\(\vec{E}\)は ――
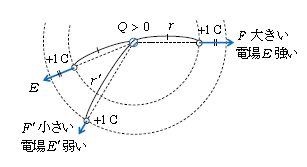
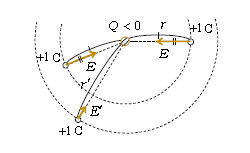
向き：\(Q\)>0のときは\(Q\)から+1Cへの斥力の向き（\(Q\)から外へと向かう向き）
\(Q\)<0のときは\(Q\)から+1Cへの引力の向き（\(Q\)から内へと向かう向き）（図２)
大きさ（あるいは電場の強さともいう。大きさを表すときは当然ベクトル記号を付けない）：クーロン則\(\displaystyle F=k\frac{|Q|×1\text{C} }{r^2} \) を1Cあたりの力\(E\)[N/C]に直すために\(F\)を1Cで割り算して \(\displaystyle E=k\frac{|Q|}{r^2} \) (☆)
つまり、クーロン則\(\displaystyle F=k\frac{|Qq| }{r^2} \)の\(|q|\)がない形だから、頭に入れやすい。
2⃣ 1Cあたりに働く力が\(\vec{E} \)ということは、2Cだったら力2×\(\vec{E}\)が働き、3Cなら3×\(\vec{E} \)…、ということで
\(q\)[C] に働く力\(\vec{F} =q×\vec{E} \) である。
ここで(☆)式を代入すると、大きさ\(\displaystyle F=|q|×k\frac{|Q|}{r^2}=k\frac{|Qq|}{r^2} \)となってクーロンの法則が復活する。つまり、電気力が1⃣ 2⃣のように2段構えで働くことによってクーロンの法則は成り立っているのである。
電荷\(Q\)が \(
\Longrightarrow \)
電場\(\vec{E}\)をつくり \(\Longrightarrow \)
大きさ\(\displaystyle E=k\frac{|Q|}{r^2} \)
電場\(\vec{E}\)が電荷\(q\)に
力\(\vec{F}\)を及ぼす
大きさ\(F=|q|E\)
\(\displaystyle =k\frac{|Qq|}{r^2} \)
さて、とかく電気現象は目に見えないのでイメージしづらい。そこで、空間の各点各点の電場ベクトル\(\vec{E}\)に次々と接していくような直線や曲線を引くことによって、電場の様子を活き活きと視覚化したものを電気力線という。電気力線の向きは\(\vec{E} \)の向き。電気力線は＋の電荷から出る。ーの電荷へと入る。電荷⊕のつくる力線、⊝のつくる力線、⊕⊝、⊕⊕、⊝⊝のつくる力線は、覚えてしまって手書きできるようにしておこう（⊕と⊝の電気量の絶対値は等しいとする 図３）。そうすれば目に見えない電気現象の理解が格段に深まる。
例えば⊕⊝の場合（図３左下）、地点Ａに置かれた+1Cに⊕が及ぼす力が斥力で青い矢印、⊝が及ぼす力が引力で黄色い矢印、それらを2辺に持つ平行四辺形をつくって合成したものが電場\(\vec{E_A}\)である。ここで「平行四辺形をつくって合成」とは、力は向きと大きさを持つベクトルだから、電場(1Cあたりに働く力)もベクトル、ゆえにベクトルの足し算をするという意味である。\(\vec{E_A}\)を特に合成電場という。電気力線は合成電場\(\vec{E_A}\)に接するように描く。
地点Bは、⊕からの距離の方が⊝からの距離より長い。電場は(☆)式の通り距離\(r\)の2乗に反比例だから、Bに置かれた+1Cに⊕から働く力(青)の方が⊝から働く力(黄)よりも小さい。合成した電場は\(\vec{E_B}\)のようになり、力線は\(\vec{E_B}\)に接している。このようにして⊕⊝のつくる力線は描かれている。
⊝⊝のつくる力線は、⊕⊕のつくる力線と概形は等しく矢印の向きが逆である。
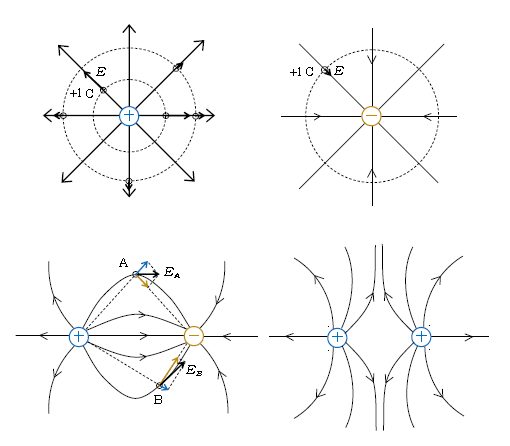
点線は補助線
なお、電気力線はある瞬間の電場の様子を視覚化したスナップショットにすぎないから、力線に沿って何か電流のようなものが流れているというイメージを持つのは良くない。