2-16-1: 屈折の法則
いろいろな現象に関わってくる屈折の法則をしっかり押さえましょう! → <例題>は2-16-2へ
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント(I) は光波に限らない全ての波についての話
ポイント(II)は光波に限った話
ポイント(I) <水面波・音波・光波など全ての波について>
屈折の法則
\(\displaystyle \frac{\sin\theta_1}{\sin\theta_2}=\frac{v_1}{v_2}=\frac{\lambda_1}{\lambda_2}=n_{12} \) (1)
(\(n_{12} \): 媒質1に対する2の相対屈折率)
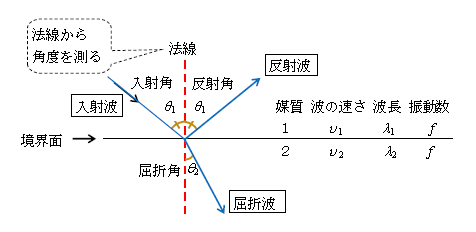
異なる媒質の境界面では反射と屈折が同時に起こる。境界面にやってくる波を入射波、はね返される波を反射波、境界面を越えていく波を屈折波という。屈折の法則(1)は2-17-1のホイヘンスの原理によって証明できる。上図にある通り、法線(境界面に立てた垂線)から角度を測ることに注意しよう(境界面から測って屈折角○○度のようには決して言わない)。なお、反射・屈折によって振動数は変化しない。 [ 振動数が1側と2側で異なるとすると、次のような不都合が生じる。媒質1側の入射波が例えば振動数10Hz、2側の屈折波が振動数5Hzだとすると、本来連続的に分布して連続的なふるまいをするはずの媒質が、境界面を境に1側と2側で不連続なふるまいをすることになる(境界面が不連続面になる)という問題が生じてしまう。屈折波と反射波についても同様の不都合が生じる。] 媒質1側も2側も振動数は同じ\(f\)だ。
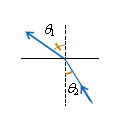
(1)の比\(\displaystyle \frac{v_1}{v_2}=\frac{\lambda_1}{\lambda_2} \)を「媒質1に対する2の相対屈折率\(n_{12} \)」という。(1)では「対する」媒質1を分子に書く(そのように相対屈折率を定義する・決める)ことに要注意。例えば光波の問題で「空気に対する水の相対屈折率を\(n\)とする」とあったら、「対する」空気を媒質1と見なして分子に書く。仮に入射側が2で屈折側が1であっても(図1)、比\(\frac{v_1}{v_2} \)自体は変わらないから、式(1)は変わらない。やはり「対する」1が分子。
ポイント(II) <光波限定>
表のように文字を決め、物質の屈折率(あるいは絶対屈折率) \(\displaystyle n=\frac{c}{c’}\) と定義する。
| 真空中 | 物質中 | |
| 光の速さ | \(c\) | \(c’\) |
| 光の波長 | \(\lambda\) | \(\lambda '\) |
・ \(c>c’\)と覚えればよく、ゆえに\(n>1\)。なお、真空の屈折率は上の定義により \(n=\frac{c}{c} =\) 1
・ \(\displaystyle n=\frac{c}{c’}=\frac{\lambda f}{\lambda ' f}=\frac{\lambda}{\lambda '} \) により \(\displaystyle c’=\frac{c}{n} \) 、 \(\displaystyle \lambda '=\frac{\lambda}{n} \) (2)
[ 屈折率\(n\)の分だけ、光速は遅くなり、波長は短くなると覚えよう]
・ 媒質1,2の(絶対)屈折率をそれぞれ\(n_1,n_2\)とすれば、
(2)より光の速さはそれぞれ \(\displaystyle v_1=\frac{c}{n_1} \) 、\(\displaystyle v_2=\frac{c}{n_2} \)
(1)に代入して \(\displaystyle \frac{\sin\theta_1}{\sin\theta_2}=\frac{\frac{c}{n_1} }{\frac{c}{n_2} }=\frac{n_2}{n_1} \) 両辺\(n_1\sin\theta_2\)倍
光波の屈折の法則 \(n_1\sin\theta_1=n_2\sin\theta_2 \) (3)
[ \(n×\sin\theta\)は一定と覚えよう ]
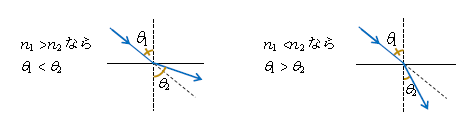
光波では、(3)のかけ算形の屈折の法則が便利なので、積極的に利用しよう。なお、例えば\(n_1>n_2\)なら、「\(n×\sin \)は一定」なので\(\sin\theta_1<\sin\theta_2 \)。つまり\(n_1>n_2\)なら\(\theta_1<\theta_2 \)。これを「\(n\)大きい方が\(\theta \)は小さい」と覚えておこう。すると光の曲がり方が簡単に判定できる(図2)。
→ <例題>は2-16-2へ