2-17-1: ホイヘンスの原理

ややもすると、とっつきづらいホイヘンスの原理を明快に解説します！　　　　　　　　　　　　　　　　　

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

　上記のホイヘンスの原理によって、波の進行の仕方、屈折・反射現象などを統一的に理解することができる

1⃣ 波の進行の仕方
　図１は、例えば海の波が進む様子を斜め上から見下ろした図。ある時刻で波面が直線になるのを平面波という（ちなみに図１を鉛直方向に拡張すれば波面は鉛直面(平面)になる）。波面と波の進行方向が垂直になる理由は、ホイヘンスの原理で説明できる。

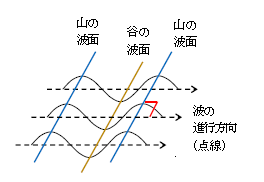
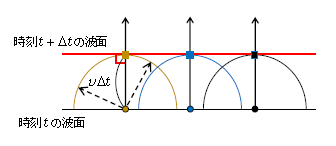
　図２は図１を真上から見て、ある時刻\(t\)での(例えば山の)波面を左右方向に示したもの。ホイヘンスの原理によれば、「まず\(t\)の波面上の各点に波源を想定する（黄色丸、青丸、黒丸）。次に、各点から半径\(v \Delta t \)(\(v\)は波の速さ)の球面波を広げる（図２のような平面図では円形波になる）。この球面波はとくに素元波と呼ばれる。最後に、これら球面波（黄、青、黒）の共通接平面(平面図では共通接線)を描くと、時刻\(t+\Delta t \)の波面が仕上がる。」以上がホイヘンスの原理の意味内容だ。ここで、たとえば黄色丸の波源からは波は球面上のどこかに行く可能性がある（点線）。しかし\(t+\Delta t \)の波面が仕上がってみると、\(t+\Delta t \)の波面上の黄色四角にたどり着くことが分かる。つまり、波の進行方向は球の半径方向。一方、半径と垂直な接平面が今まさに波面なのだから、波面と波の進行方向は垂直というわけである。

2⃣ 屈折
　次に2-16-1で扱った屈折の法則をホイヘンスの原理から導こう。図３の上側が媒質１、下側が媒質２で、それぞれの波の速さ\(v_1,v_2\)、波長\(\lambda_1,\lambda_2\)、振動数\(f\)が示してある（2-11-1でやった通り、媒質１、２の振動数\(f\)は共通）。入射波の進行方向に垂直な波面PQの中点をMとする。波がPQに到達した時刻を\(t=0\)とし、Q’へ到達した時刻を\(t\)とする（ゆえにQQ’=\(v_1 t\)）。M’’に到達する時刻は中点連結の定理より\(\frac{t}{2}\)。P(\(t=0\))を中心とする素元波は、時刻\(t\)には媒質２側で半径\(v_2 t\)の球面波として広がる（黄色）。M"(時刻\(\frac{t}{2}\))を中心とする素元波は、時刻\(t\)には媒質２側で半径\(\frac{1}{2} v_2 t\)の球面波として広がる（青）。よって、時刻\(t\)の波面は共通接平面としてのP’Q’。この波面に垂直に進むのが屈折波だ。
　[　ここでPを中心とする黄色い円（大円と呼ぶ）に対する接線P’Q’は、M’’を中心とする青い円（小円）にも接していることに注意。理由は ―― M’’からPP’に平行に引いた線とP’Q’との交点をM’とすると（このときM’が小円上に乗っているかどうかはまだ分からない）
　∠M’’M’Q’=90°　　∴　△M’’M’Q’∽△PP’Q’＝1:2 　　∴　M’M’’=\(\frac{1}{2}\)PP’=\(\frac{1}{2} v_2 t \)
　したがってM’は小円上にあることになり, 小円とP’Q’との接点であると言える。　]

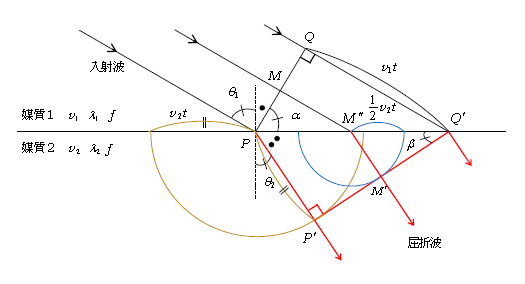
　さて、屈折の法則を証明しよう。図３の左右方向に引いた境界に法線（点線）を立てて、法線から入射角\(\theta_1\)、屈折角\(\theta_2\)を測る。
　いまPQ’＝\(d\)とおくと、図３の\(\displaystyle \sin\alpha =\frac{\text{QQ′} }{\text{PQ′}}=\frac{v_1 t}{d}\)
　　　　　　　　　　　　　　 \(\displaystyle \)\(\displaystyle \sin\beta =\frac{\text{PP′} }{\text{PQ′}}=\frac{v_2 t}{d}\)
　2式割り算　\(\displaystyle \frac{\sin\alpha}{\sin\beta} =\frac{v_1 t}{d}\frac{d}{v_2 t}=\frac{v_1}{v_2}\)
　ここで、\(\alpha =\theta_1 \)（\(\alpha \)+●=90° かつ ●+\(\theta_1 \)=90°だから）、\(\beta =\theta_2　\)（直角三角形PP’Q’の直角以外の２角の和は90°のため\(\beta \)+●●=90° かつ ●●+\(\theta_2 \)=90°だから）であることを用いると、
　\(\displaystyle \frac{\sin\theta_1}{\sin\theta_2} =\frac{v_1}{v_2}=\frac{\lambda_1 f}{\lambda_2 f}=\frac{\lambda_1}{\lambda_2} \)　　　よって屈折の法則が証明された。