2-21-1: 2スリットの干渉(ヤングの干渉実験)
ここで2-09-1で扱った干渉を、光波に応用してみましょう! → <例題>は2-21-2へ
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント
・ ヤングの干渉実験
経路差=図1中の☆
\(\displaystyle =d\sin\theta ≒d\tan\theta =d\frac{x}{l} \) (1)
強め合いの条件は 経路差\(\displaystyle d\frac{x}{l} =m\lambda \: \) (2)
(\(m=0,\pm 1,\pm 2,\cdots \) ; \(\lambda\)は光の波長)

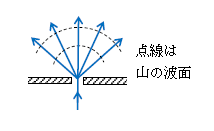
まず前提として、目に見える光(可視光)の波長\(\lambda\)は10\(^{-7} \)m程度とひじょうに短いが、今まで同様に波として扱える。光に限らず全ての波は、すきまや障害物を通過後、直進するだけでなく様々な方向に広がって進む(図2)。これを回折という。波動独特の性質だと思えばよい(回折をホイヘンスの原理に基づいて理解することもできる)。
ヤングの干渉実験(ヤングは人名)を3次元的に見てみよう(図3)。光をスリット(細いすきま)S0に通して回折させ、スリットS1、S2に到達させると、等距離S0S1=S0S2であるため、S1に光が山で届くときにはS2にも山で届く。つまりS1、S2は「同位相の波源」と見なせる。S1、S2で光は再び回折し、スクリーン上で干渉する(強め合ったり弱め合ったりする)。光は強め合うと明るく、弱め合うと暗く見える。
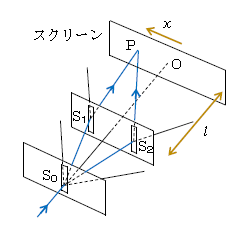
同位相の波源の場合、強め合いの条件は図3で
経路差S2P\(-\)S1P=\(m\lambda \)(\(m=0,\pm 1,\pm 2,\cdots \);\(\lambda \)は光の波長) (1)
この条件を満たす点Pには明線が写る。弱め合いは
S2P\(-\)S1P=\( (m+\frac{1}{2} )\lambda \)
これを満たす点Pには暗線が写る。結論から言うと、スクリーン上には明線と暗線が交互に等間隔で並んだ干渉縞が生じる(図6)(図1、図3、図6の\(x\)軸は全て対応している)。ヤングの干渉実験は、よく「2スリットの干渉」とも呼ばれる。
経路差を求めるために、図3を天井から見た図4のような作図をする。S2P上に点QをS1P=QPとなるように取れば、経路差S2P\(-\)S1PはS2Qに等しい。ところがヤングの実験では、S1S2を通るスリット面からスクリーンまでの距離\(l\)が1m規模なのに対し、スリットS1とS2の間隔\(d\)は1mm規模、つまり\(l\)は\(d\)に比べて1000倍も遠い。すると二等辺三角形S1PQの頂角はほぼ0°、両底角\(\alpha\)はほぼ90°となり、S1PとS2Pをほぼ平行と見なして、図1の説明文中にあるような平行光線近似の作図をしてよくなる。S1、S2付近を拡大すれば図5のようになり、
\(\displaystyle \)\(\theta\)+●=\(\angle\)S1MN=90° ∴ ●=90°\(-\theta\)
直角三角形MS1Rで \(\angle\)MS1R+●=90° これにすぐ上の●を代入
\(\angle\)MS1R+90°\(-\theta\)=90° ゆえに \(\angle\)MS1R=\(\theta\)であることが分かる。
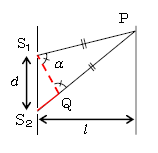
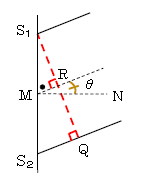
図1に戻ると、 経路差=☆印の距離\(=d\sin\theta\)
ここでヤングの実験での角\(\theta\)は十分小さい(光の回折に関わる理由があり、ここでは説明しない)。十分小さい角度\(\theta\)について\(\sin\theta ≒\tan\theta \)(なぜなら\(\theta\)が十分小さいと\(\cos\theta \)≒1だから\(\tan\theta =\frac{\sin\theta}{\cos\theta} ≒\sin\theta \))であることを用いると、
経路差=\(\displaystyle d\sin\theta ≒ d\tan\theta =d\frac{x}{l} \)
強め合いの条件は(1)より、経路差\(\displaystyle d\frac{x}{l} =m\lambda \)
これを\(x\)について解くと、明線の位置\(\displaystyle x=m\frac{l\lambda}{d} \)と求まるが、通常\(x\)に添え字\(m\)を付けて\(x_m\)と表し、 \(\displaystyle x_{3}=3\frac{l\lambda}{d},\: x_{-2}=-2\frac{l\lambda}{d} \) (数列の一般項)のように扱う。
ゆえに明線の位置は \(\displaystyle x_m=m\frac{l\lambda}{d}\)
(\(\displaystyle x_0=0, \, x_{\pm 1}=\pm\frac{l\lambda}{d},\, x_{\pm 2}=\pm2\frac{l\lambda}{d},\, \cdots \)) (複号同順)
これは数列で言えば等差数列だから、図6のような等間隔の干渉縞が得られることになるのだ。
なお、\(x_0, x_{\pm 1}, x_{\pm 2}, \cdots \)を順に0次,\(\pm 1\)次,\(\pm 2\)次,\(\cdots \)の明線と通常呼ぶ。
→ <例題>は2-21-2へ



