2-25-2: 回折格子 ＜例題＞

例題を通じて回折格子の理解を深めましょう！　　　　　　　　　　　　　　　　　　　　　　　

例題　

　ガラス板の片面に多数の平行な溝を等間隔に引いた回折格子があり、その格子定数を\(d\)とする。まず、図１のように左からガラス面に垂直に波長\(\lambda \)の単色光を入射させる。回折した光が強めあって明線を作るときの角度を\(\theta\)とする。

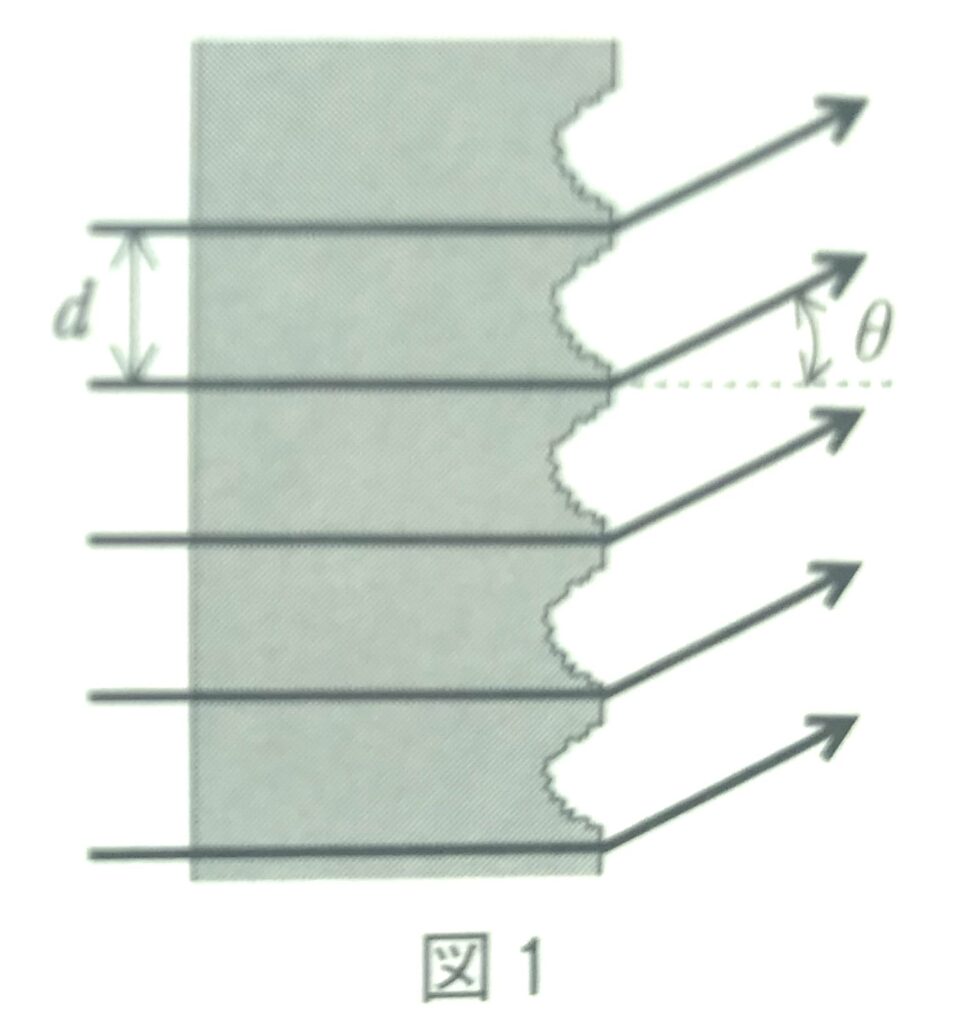
問１　角度\(\theta\)はどのような式で表わされるか。次の①～④のうちから正しいものを一つ選べ。ただし\(　m=0,\pm 1,\pm 2,\cdots\ \)とする。
①　\(\displaystyle \sin\theta =\frac{md}{\lambda} \)　　②　\(\displaystyle \cos\theta =\frac{md}{\lambda} \)　　③　\(\displaystyle \sin\theta =\frac{m\lambda}{d} \)　　
\(\displaystyle \)④　\(\displaystyle \cos\theta =\frac{m\lambda}{d} \)

　次に、図２のように回折格子の左右の向きを入れ換え、左からガラス面に垂直に波長\(\lambda \)の単色光を入射させる。左面の回折格子で回折した光はガラスの中を進み、そののち空気中を進む。

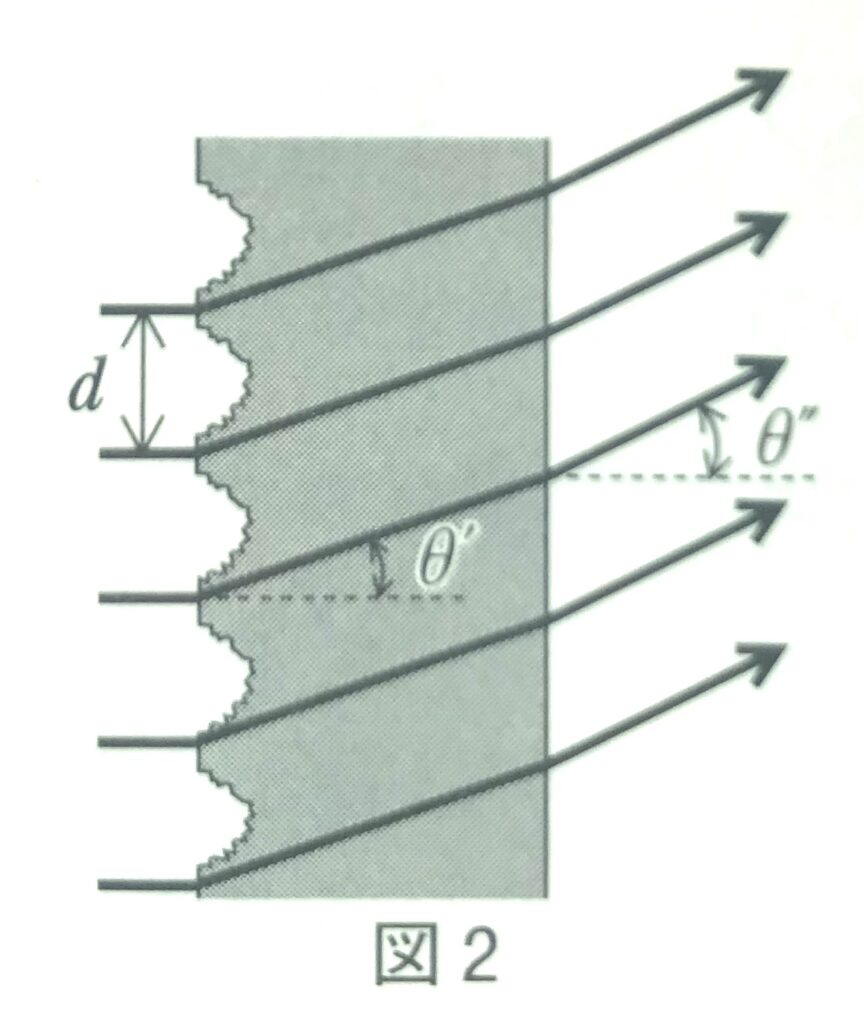
問２　ガラスから空気中に進んだ回折光が明線を作るときの角度\(\theta’’ \)はどのような式で表わされるか。次の①～⑥のうちから正しいものを一つ選べ。ただし\(m=0,\pm 1,\pm 2,\cdots\ \)とする。
①　\(\displaystyle \sin\theta’’ =\frac{md}{\lambda} \)　　②　\(\displaystyle \cos\theta’’ =\frac{md}{\lambda} \)　　③　\(\displaystyle \cos\theta’’ =\frac{nmd}{\lambda} \)　
④　\(\displaystyle \sin\theta’’ =\frac{m\lambda}{d} \)　　⑤　\(\displaystyle \sin\theta’’ =\frac{nmd}{\lambda} \)　　⑥　\(\displaystyle \cos\theta’’ =\frac{m\lambda}{d} \)

解答・解説

問１　強め合いの条件は2-25-1より\(d\sin\theta =m\lambda \)
　　　∴　　\(\displaystyle \sin\theta =\frac{m\lambda}{d} \)　　　　答　③
問２　起こっている現象を図３で説明しよう。まず点Aでスリットを通過するから回折が起こる。次に点Bでは、スリット(細いすきま)ではなく、広くなめらかなガラス面を通過するから回折は起きず、その代わり屈折が起こる。回折と屈折の違いは ―― 回折はいろいろな方向へ広がる現象だから\(\theta’ \)は変数。屈折は屈折の法則に従うから、１つの入射角\(\theta’ \)に対して屈折角\(\theta’’ \)は１つに決まる。

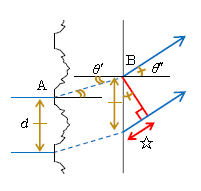
　さて、強め合いの条件を求めたいので、経路差を求めよう。図３の点線どうしの距離は等しいから、経路差=☆=\(d\sin\theta’’ \)。よって強め合いの条件は \(d\sin\theta’’ =m\lambda \)　　
　∴　\(\displaystyle \sin\theta’’ =\frac{m\lambda}{d} \)　　　　答　④