2-07-4: 定常波の波の式 (続き)

2-07-3で導いた定常波の波の式の物理的意味を明快に解説します！　　　　　　

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

　前の単元2-07-3の(5)の式を、番号①②付きで再掲しよう。
　定常波の式\(Y(x,t)=\)\(\displaystyle \left[ ①\: 2A\cos\left( 2\pi \frac{x}{\lambda} \right) \right] \) × \(\displaystyle \left[ ②\: \sin\left( 2\pi \frac{t}{T} \right) \right] \)　　　 (5)
　(5)は2つの三角関数の積で表されていて、①は\(x\)のみの関数、②は\(t\)のみの関数になっている（「変数分離形」と言ったりもする）。この式は次のように考えれば何と(！)グラフ化できる。まず(5)を
　「定常波の高さ\(Y\)は（①の高さ）×（②の値）」　(☆)
のように読むことにする。以下1⃣2⃣ の順序で説明していこう。
　1⃣　（①の高さ）は\(x\)の関数だから\(y\)-\(x\)グラフ（波形）として図示できる。
　2⃣　（②の値）は\(\sin\)関数だから\(-1≦\)②\(≦1\)の値域を取る。　　
　1⃣　(5)中の（①の高さ） \(\displaystyle y=2A\cos\left( 2\pi \frac{x}{\lambda} \right) \) のグラフは図１の赤線のようになる。\(\cos\)の中身\(\displaystyle 2\pi \frac{x}{\lambda} \)の\(x\)に\(\lambda\)を代入すると、\(\cos\)の中身が\(2\pi\)になる。\(2\pi\)はコサインカーブ1個分に対応するから、図１は\(\lambda\)が1波長分になっている\(y\)-\(x\)グラフである。図１にはその上下逆さまのグラフを青で、高さが0のままのグラフを緑で図示しておいた。
　2⃣　(5)中の（②の値）\(\displaystyle =\sin\left( 2\pi \frac{t}{T} \right) \)であるが、\(t\)に順次\(\displaystyle 0,\frac{T}{4},\frac{T}{2},\frac{3T}{4}\)を代入していこう。
　　\(t=0\)のときは （②の値）\(\displaystyle =\sin\left( 2\pi \frac{0}{T} \right)=0 \) 。　このとき(☆)より「定常波の高さ\(Y\)は（①の高さ(図１赤)）×\(0=0\)」。ということは、\(t=0\)に写真を取ると、いたる所の\(x\)で高さが\(0\)の緑のグラフが写ることになる。
　　\(\displaystyle t=\frac{T}{4}\)のときは（②の値）\(\displaystyle =\sin\left( 2\pi \frac{\frac{T}{4}}{T} \right)=\sin\frac{\pi}{2}=1 \) 。「定常波の高さ\(Y\)は（①の高さ）×\(1=\)（①の高さ(図１赤)）」。つまり\(\displaystyle t=\frac{T}{4}\)に写真を取ると、赤いグラフが写る。
　　\(\displaystyle t=\frac{T}{2}\)のときは （②の値）\(\displaystyle =\sin\left( 2\pi \frac{\frac{T}{2}}{T} \right)=0 \) 。\(\displaystyle t=\frac{T}{2}\)では高さが\(0\)の緑のグラフが写る。
　　\(\displaystyle t=\frac{3T}{4}\)のときは （②の値）\(\displaystyle =\sin\left( 2\pi \frac{\frac{3T}{4}}{T} \right)=\sin\frac{3\pi}{2}=-1 \) 。「定常波の高さ\(Y\)は（①の高さ）×\((-1)\)」。\(\displaystyle t=\frac{3T}{4}\)では赤の上下逆さまの青いグラフが写る。

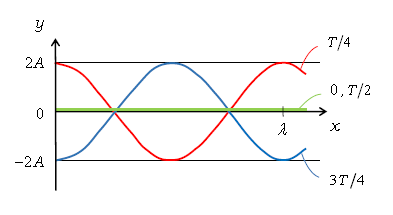
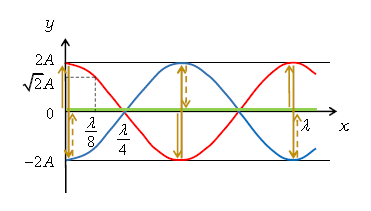
　あとは時間の順序 \(\displaystyle t=0,\frac{T}{4},\frac{T}{2},\frac{3T}{4},\cdots\) に従って、緑、赤、緑、青、… のように\(y\)-\(x\)グラフを動かせば、図２のような「動画」が見られる。これはまさに2-07-1で示した通りの定常波のふるまいである。

　最後になるが、(5)定常波の式中の\(x\)のみの関数の項は
　（①の高さ）\(\displaystyle =2A\cos\left( 2\pi \frac{x}{\lambda} \right) \) 　　　　　　　　　　　　　 (6)
で、それは図１(または図２)の赤いグラフの高さだから、その絶対値は振幅を表す。(6)を見ての通り、振幅は位置\(x\)ごとに異なる。例えば、図２の腹の位置\(x=0\)と節の位置\(\displaystyle x=\frac{\lambda}{4}\)の中点\(\displaystyle x=\frac{\lambda}{8}\)では、
　振幅\(=\)(6)の絶対値\(\displaystyle =2A\left| \cos\left( 2\pi \frac{\frac{\lambda}{8}}{\lambda} \right) \right| =2A\cos\frac{\pi}{4}=\sqrt{2}A \)　である。