2-03-3: 波の式 <例題>
例題を通じて波の式の扱い方を練習しておきましょう! → 波の式 の説明は2-03-1へ
例題
\(x\)軸に沿って進む正弦波がある。図1で横軸は位置\(x\)、縦軸は媒質の変位\(y\)を表す。図1は時刻\(t=0\)における位置\(x=l\)(\(l>0\))付近のグラフで、\(x=l\)にて\(y=0\)である。波の振幅を\(A\)、周期を\(T\)、波長を\(\lambda\)とする。
問1 この波が\(+x\)方向に進む波であるとき、位置\(x=l\)における時刻\(t\)での変位\(y\)を求めよ。
問2 この波が\(-x\)方向に進む波であるとき、位置\(x\)における時刻\(t\)での変位\(y\)を求めよ。
問3 この波が\(-x\)方向に進む波であるとし、\(\displaystyle l=\frac{5\lambda}{8} \)であるとする。位置\(x=0\)における時刻\(\displaystyle t=\frac{T}{2}\)での変位\(y\)を求めよ。
解答・解説
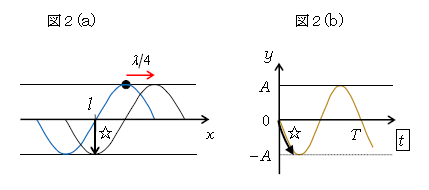
問1 問題文「位置\(x=l\)における時刻\(t\)での変位\(y\)」とは\(x=l\)での振動の式という意味。そこで、2-02-2のポイント「波形\(y\)-\(x\)グラフを\(\frac{1}{4} \)波長動かすと、振動\(y\)-\(t\)グラフの\(\frac{1}{4} \)周期分が分かる」を利用する(図2(a))。図1を山●に目印を付けて\(\frac{1}{4} \)波長動かす。\(x=l\)の粒子に注目すれば、☆のように下向きに動く。この動きを横軸を\(t\)として追うと、図2(b)のような\(y\)-\(t\)グラフが書ける。これは\(-\sin\)型のグラフだから、2-03-1の(*)の式と同様に
答 \(\displaystyle y=-A\sin\frac{2\pi}{T} t \)
問2 問題文「位置\(x\)における時刻\(t\)での変位\(y\)」とは波の式\(y(x,t)\)という意味。そこで2-03-1の1⃣2⃣3⃣ の手順に従う。
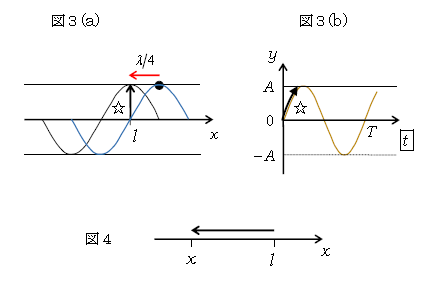
1⃣ \(x=l\)での振動の式を得るために、問1と同様のことをやる。ただし、今度は図1の波形\(y\)-\(x\)グラフを\(-x\)方向に\(\frac{1}{4} \)波長動かす(図3(a))。\(x=l\)の粒子は☆のように上向きに動く。すると図3(b)のような\(y\)-\(t\)グラフが書ける。これは\(+\sin\)型のグラフだから、
\(x=l\)での振動 \(\displaystyle y=A\sin\frac{2\pi}{T} t \) (1)
2⃣ \(x=l\)から\(x\)まで\(-x\)方向に波の伝わる時間\(t’\)は、図4を見ると分かる通り
\(t’=\)距離÷速さ\(\displaystyle =\frac{l-x}{V} \)
3⃣ 波の式\(y(x,t)\)は(1)の\(t\)を\(t-t’\)におきかえたものに等しいから、
\(\displaystyle y(x,t)=A\sin\frac{2\pi}{T} (t-t’)=A\sin\frac{2\pi}{T} \left( t-\frac{l-x}{V} \right) \)
ただし\(V\)は問題文中に与えれていない文字だから、\(\displaystyle V=\frac{\lambda}{T}\)と書きかえて、
波の式\(y(x,t)=\) 答 \(\displaystyle A\sin2\pi \left( \frac{t}{T}-\frac{l-x}{\lambda} \right) \) (2)
問3 (2)に\(\displaystyle l=\frac{5\lambda}{8} \)を代入して
波の式\(\displaystyle y(x,t)=A\sin2\pi \left( \frac{t}{T}-\frac{\frac{5\lambda}{8}-x}{\lambda} \right) \)
\(\displaystyle =A\sin2\pi \left( \frac{t}{T}+\frac{x}{\lambda} -\frac{5}{8} \right) \, \) (3)
問題文に「\(x=0\)における\(\displaystyle t=\frac{T}{2}\)での\(y\)」とあるから、(3)に\(x=0\)、\(\displaystyle t=\frac{T}{2}\)をインプットして
\(\displaystyle y \left( 0,\frac{T}{2} \right) =A\sin2\pi \left( \frac{\frac{T}{2}}{T}-\frac{5}{8} \right) \)\(\displaystyle =A\sin \left( -\frac{\pi}{4} \right)\)
∴ \(\displaystyle y \left( 0,\frac{T}{2} \right) = \) 答 \(\displaystyle -\frac{A}{\sqrt{2}} \)
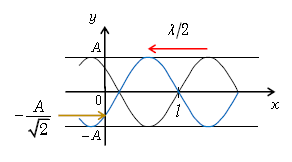
・ 参考までに、\(\displaystyle l=\frac{5\lambda}{8}=\frac{\lambda}{4}÷2+\frac{\lambda}{2}\)の場合の波形\(y\)-\(x\)グラフを図5に示す。\(t=0\)の波形が黒のグラフ。\(\displaystyle t=\frac{T}{2}\)では波形が\(-x\)方向に\(\displaystyle \frac{\lambda}{2} \)移動して(波形が上下逆さまになって)青のグラフ。青のグラフの\(x=0\)の変位が答の\(\displaystyle y=-\frac{A}{\sqrt{2}} \) である。