2-02-2: y-xグラフとy-tグラフ <例題>
さっそく波動分野の例題1題目に入りましょう!
ポイント
・ 波形\(y\)-\(x\)グラフを\(\frac{1}{4} \)波長動かすと、
振動\(y\)-\(t\)グラフの\(\frac{1}{4} \)周期分が分かる
例題
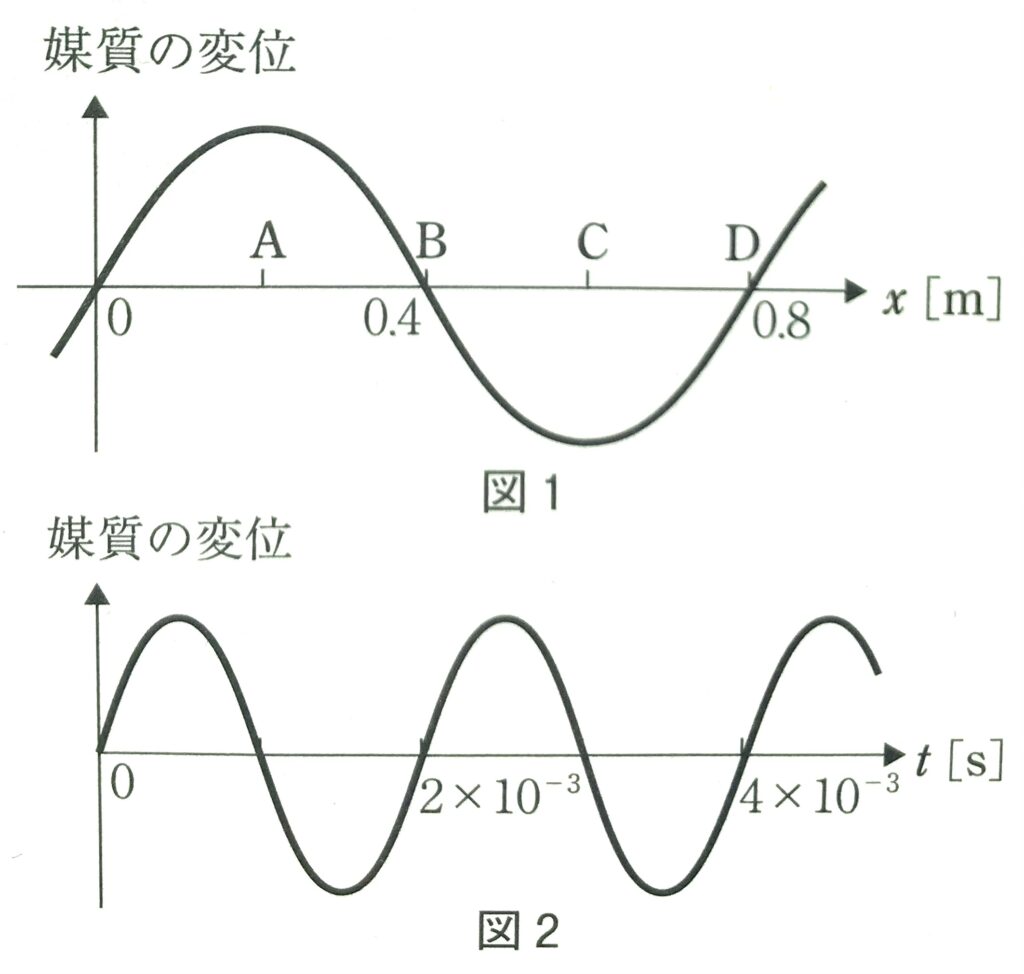
\(x\)軸に沿って進む波がある。図1は時刻\(t=0\)における場所ごとの媒質の変位を表したグラフである。図2は場所\(x=0\)における媒質の変位の時間変化を表したグラフである。この波の速度はほぼ何m/sになるか。次の①~⑥のうちから正しいものを一つ選べ。
① \(-\)800 ② \(-\)400 ③ \(-\)200 ④ 200 ⑤ 400 ⑥ 800
解答・解説
横軸が[m]単位の\(y\)-\(x\)グラフ(図1)からは、波長\(\lambda \)[m]が読み取れる: \(\lambda\)=0.8m
横軸が[s]単位の\(y\)-\(t\)グラフ(図2)からは、周期\(T\)[s]が読み取れる: \(T\)=2×10\(^{-3}\)s
ゆえに波の速さ\(\displaystyle V=\frac{\lambda}{T}=\frac{0.8 \text{m}}{2×10^{-3} \text{s}} =400\)m/s (*)
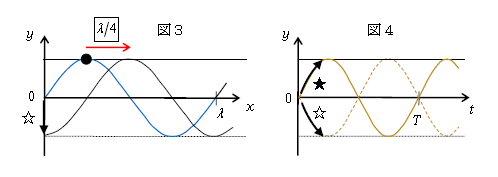
ただし、波の「速さ」ではなく「速度」はいくらかと聞かれたので、速度の符号、つまり波の進む向きを見極めよう。そのためには、実際に波形(\(y\)-\(x\)グラフ)(図3)を\(+x\)方向や\(-x\)方向に動かしてみるとよい。動かすときには、山●に目印を付けて\(\frac{1}{4} \)波長動かすのが分かりやすい。また、図2は\(x=0\)に固定した\(y\)-\(t\)グラフだから、\(x=0\)の粒子に注目しよう。
\(+x\)方向に動かすと、\(x=0\)の粒子が図3☆のように下向きに動くから、\(y\)-\(t\)グラフは図4の点線のようになる。
\(-x\)方向に動かすと\(x=0\)の粒子が図5★のように上向きに動くから\(y\)-\(t\)グラフは図4の実線のようになる。
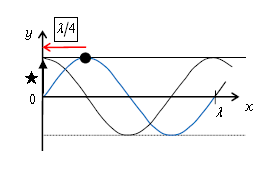
図2と一致するのは図3の実線の方だから、\(-x\)方向に動かした図5の場合に相当する。よって波の速度は負の向きで、その値は(*)より \(-400\)m/s 答 ②


