2-03-1: 波の式 ＃その１

学生がつまづきやすい波の式のつくり方を明快に解説します！　　→　＜#その２＞は2-03-2へ　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

　まず導入として、力学の大目的とは何だったか振り返る。1-06-1で述べた通り、それは物体の運動を調べること。とりわけ任意の時刻\(t\)での位置\(x\)が求まれば、力学的現象の本質は記述できたようなものである（図１(a)）。では波動現象の本質を記述するにはどうすればいいか。それには、任意の時刻\(t\)及び任意の位置\(x\)で波の変位(高さ)\(y\)を求めればよい（図１(b)）。全ての位置\(x\)について全ての時刻\(t\)にわたり高さ\(y\)が分かったなら、波動の本質は記述できている。
　ところで数学では\(x\)の関数を\(f(x)\)と書く。この記号を用いて、力学の「任意の時刻\(t\)での位置\(x\)」は\(x(t)\)と書く。波動の「任意の位置\(x\)及び任意の時刻\(t\)での変位\(y\)」は\(y(x,t)\)のように表す。\(y\)が\(x\)及び\(t\)の関数であるという意味だ。この\(y(x,t)\)は広く「波の式」と呼ばれている。波動を完全に記述する式であると表現しておく。

　さて、波の式\(y(x,t)\)をどうやって求めるか。以下3部構成でその手順を説明していこう。
1⃣　波動を完全に記述する波の式\(y(x,t)\)が、何の手掛かりもなく求まるはずもない。そこで足掛かりとして、ある1点\(x_0\)の媒質粒子の単振動の式を出発点にしよう。\(x_0\)の振動の式とは、位置\(x_0\)、時刻\(t\)での粒子の高さ(したがって波の変位)\(y\)を表す式に他ならないから\(y(x_0,t)\)と書ける。いま
　\(y(x_0,t)=A\sin\omega t\)　　　　(＊)
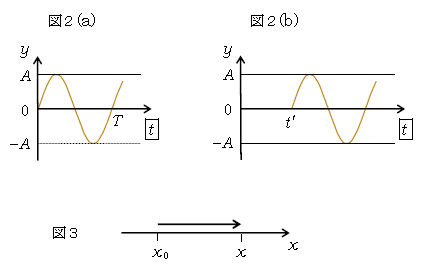
であるとする。(＊)は1-23-1で扱った単振動の式\(x=A\sin\omega t\)（\(\phi=0\)かつ中心\(x_c=0\)の場合）で、ただし左辺は\(x\)ではなく \(y(x_0,t)\)としたもの。そのグラフは図２(a)のようになる。ここで周期\(\displaystyle T=\frac{2\pi}{\omega} \) だから \(\displaystyle \omega=\frac{2\pi}{T} \) 。これを(＊)に代入して
　\(x_0\)の振動 \(\displaystyle y(x_0,t)=A\sin\frac{2\pi}{T} t \)　　　　　　　　　　　　　　　　　　(1)
波動では周期\(T\)を用いたこの振動の式をよく使う。
2⃣　2-01-1の通り、波動では「1点の振動が少しずつ遅れたタイミングで隣りの隣りの振動を引き起こし」ながら波が伝わる。\(x_0\)の振動は別の位置\(x\)（任意の\(x\)とする）に遅れて伝わる。波の速さを\(V\)とすれば、\(x_0\)から\(x\)まで波の伝わる時間\(t’\)\(=\)距離÷速さ\(\displaystyle =\frac{x-x_0}{V}\)（図３）。
3⃣　すると位置\(x\)のグラフは図２(b)のようになる。つまり、(a)のように\(t=0\)で\(\sin\)型のグラフが始まるのではなく、(b)では振動のタイミングが\(t’\)だけ遅れて\(t’\)で\(\sin\)型が始まる（もう1度2⃣を読んでほしい）。このとき(b)を表す式は位置\(x\)の振動で、これは位置\(x\)、時刻\(t\)での粒子(波)の高さ\(y\)に等しいから\(y(x,t)\)と書ける。すなわち(b)の式こそ求めたい「波の式」\(y(x,t)\)だ。ところで(b)は(a)を\(t\)軸に沿って\(t’\)平行移動したグラフだから、(b)を数式で表すには(a)の式(1)中の\(t\)を\(t-t’\)で置き換えればよい（数学で学ぶ平行移動の手続き）。よって
　波の式 \(\displaystyle y(x,t)=A\sin\frac{2\pi}{T} (t-t’) =A\sin\frac{2\pi}{T} \left( t-\frac{x-x_0}{V} \right) \, \)　　(2)
　以上、ここまでの「波の式のつくり方」がポイントにまとめてある。

　この単元冒頭の第2段落で、波の式とは波動を完全に記述する式であると述べた。例えば位置\(x=\)3mの時刻\(t=\)5sのことを調べたかったら、\(x=\)3m 、\(t=\)5sを(2)にインプットすると、高さ\(y\)がアウトプットされる。まさにどんな\(x\)もどんな\(t\)もカバーできる完全対応型の式が波の式である。
　ここで\(x_0\)を原点に選ぶと、(2)は
　波の式 \(\displaystyle y(x,t)=A\sin\frac{2\pi}{T} \left( t-\frac{x}{V} \right) \)　　
となる。次の単元2-03-2では、この式を題材にしてさらに波の式の説明を続けていくことにしたい。