2-03-2: 波の式 #その2
さらに波の式の理解を深めましょう! → <#その1>は2-03-1、<例題>は2-03-3へ
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント
・ 原点の振動の式 \(\displaystyle y(t)=A\sin\left( \frac{2\pi}{T} t +\phi \right) \) に対して、
\(\pm x\)方向に伝わる波の式\(y(x,t)\)は(以下複合同順とする)
\(\displaystyle y(x,t) =A\sin\left[ \frac{2\pi}{T} \left( t \mp \frac{x}{V} \right) +\phi \right] \)\(\displaystyle =A\sin\left[ 2\pi \left( \frac{t}{T} \mp \frac{x}{\lambda} \right)+\phi \right]\)
・ 波の式\(y(x,t) \)で
\(x=x_1\)に固定すると\(x_1\)での振動すなわち\(y\)-\(t\)グラフが扱える。
\(t=t_1\)に固定すると\(t_1\)での波形すなわち\(y\)-\(x\)グラフが扱える。
前の単元2-03-1で\(x_0\)の振動の式\(\displaystyle y(x_0,t)=A\sin\omega t\) としたが、ここでは\(x_0\)を原点に選び、さらに原点の振動の式\(y(0,t)\)を単に\(y(t)\)と書くことにする。すなわち
\(\displaystyle y(t)=A\sin\omega t\) (*)
すると2-03-1最後にあるように、
波の式 \(\displaystyle y(x,t)=A\sin\frac{2\pi}{T} \left( t-\frac{x}{V} \right) \) (1)
まずは(1)を少し式変形してみよう。\(\sin\)の中身にある\(T\)をカッコの中に移すと
\(\displaystyle y(x,t)=A\sin2\pi \left( \frac{t}{T}-\frac{x}{VT} \right) \)
波の速さ\(\displaystyle V=\frac{\lambda}{T}\)(2-01-1)より\(VT=\lambda\) を代入すると
波の式 \(\displaystyle y(x,t) =A\sin2\pi \left( \frac{t}{T}-\frac{x}{\lambda} \right) \; \) (2)
これも(1)と同様、波の式としてよく現れる形である。ところで(2)の\(\sin\)の中身を位相(1-23-1)といい、その単位はrad(ただし1-19-11⃣で説明した通り、radは事実上単位がないのと同じである)。確かに(2)のカッコの中は\(t\)[s]を\(T\)[s]で割って単位のない形、\(x\)[m]を\(\lambda\)[m]で割って単位なしの形になっている。ということは、カッコの中に例えば\(\displaystyle \frac{t}{\lambda}\)[s/m] や\(xT\)[m\(\cdot\)s] のような項が現れることはない。これが分かっていれば、波の式の形は頭に入れやすいだろう。
次に\(-x\)方向に進む波の式をつくろう。2-03-1の1⃣2⃣3⃣ の手順に従う。
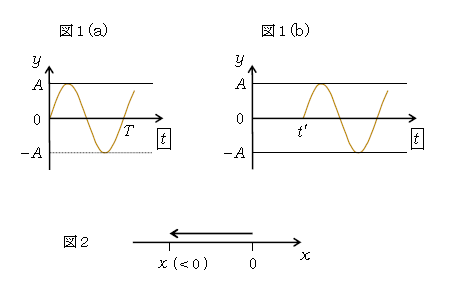
1⃣ 原点の振動\(y(t)\)は(*)(図1(a)) 。
2⃣ 波の伝わる時間\(t’\)には注意が必要だ。波が\(-x\)方向に進むということは、図2を見ての通り任意の\(x\)が\(x\)軸の負側に設定される。このように\(x<0\)のとき、原点\(x=0\)からの距離は\(|x|=-x\) だから、伝わる時間\(t’=\)距離÷速さ\(\displaystyle =\frac{-x}{V} \) 。念を押すが、\(x<0\)だから\(\displaystyle t’=\frac{-x}{V}>0\)である。
3⃣ 原点よりも\(x\)の方が振動のタイミングが\(t’\)だけ遅れて\(t’\)で\(\sin\)型が始まる(図1(b))。このとき(b)を表す式は位置\(x\)、時刻\(t\)での粒子(波)の高さ\(y(x,t)\)すなわち波の式である。ところで(b)は(a)を\(t\)軸に沿って\(t’\)平行移動したグラフだから、(b)の式\(y(x,t)\)は(a)の式(*)中の\(t\)を\(t-t’\)で置き換えたものに等しく、
波の式 \(\displaystyle y(x,t)=A\sin\frac{2\pi}{T} (t-t’) =A\sin\frac{2\pi}{T} \left( t+\frac{x}{V} \right) \)
\(\displaystyle =A\sin2\pi \left( \frac{t}{T}+\frac{x}{\lambda} \right) \, \) (3)
(1)(2)と(3)を見比べると、\(+x\)方向に進む波の式では\(\sin\)の中身の\(t\)と\(x\)が逆符号で入る一方、\(-x\)方向に進む波では同符号で入っている。
ところで、(1)の振動の式は一般的には初期位相\(\phi\)を含めて
\(\displaystyle y(0,t)=A\sin\left( \frac{2\pi}{T} t +\phi \right) \)
である。すると、以下複合同順として\(\pm x\)方向に伝わる波の式\(y(x,t) \)の一般形は
\(\displaystyle y(x,t) =A\sin\left[ \frac{2\pi}{T} \left( t \mp \frac{x}{V} \right) +\phi \right] \)\(\displaystyle =A\sin\left[ 2\pi \left( \frac{t}{T} \mp \frac{x}{\lambda} \right)+\phi \right]\)
となる。
最後に、波の式の理解を深める話をしよう。題材として
(2)の式 \(\displaystyle y(x,t) =A\sin2\pi \left( \frac{t}{T}-\frac{x}{\lambda} \right) \, \) (2)
を扱う。さて、2-03-1の最後の方で、波の式\(y(x,t)\)はどんな\(x\)、どんな\(t\)をインプットしても高さ\(y\)がアウトプットされる完全対応型の式であると述べた。
そこでまず、\(x=0\)をインプットしてみる。このインプット(代入)の作業は、本来なら変数の\(x\)が\(x=0\)という1つの値に定まってしまうから、\(x=0\)に「固定する」とよく表現される。(2)より
\(\displaystyle y(0,t) =A\sin \frac{2\pi}{T} t \)
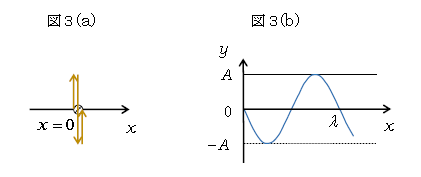
これは明らかに\(x=0\)での振動の式である。というのも、\(x=0\)に「固定する」と、\(x=0\)の粒子だけを見つめ続けて他の位置\(x\)を見ないことになる。あとは\(t\)を変数として\(t=\)1s,2s,…と変えていけば、原点\(x=0\)の粒子の振動が追えるというわけだ(図3(a))。全く同様に、\(x=x_1\)に固定すると\(x_1\)の振動\(y(x_1,t)\)あるいは\(x_1\)での\(y\)-\(t\)グラフが扱える。 (☆1)
次に\(t=0\)に固定してみる。(2)より
\(\displaystyle y(x,0) =A\sin2\pi \left( -\frac{x}{\lambda} \right)=-A\sin \frac{2\pi}{\lambda} x \) (4)
このグラフを横軸\(x\)で表すと図3(b)のようになる。(4)の\(x\)に\(\lambda\)を代入すると\(\sin\)の中身が\(2\pi\)になり、\(2\pi\)はサインカーブ1個分に対応するから、図3(b)は\(\lambda\)が1波長分になっている\(y\)-\(x\)グラフである。つまり、\(t=0\)に固定すると、まさに\(t=0\)の瞬間写真を撮ったかのように波形のグラフが書けるというわけだ。同様に、\(t=t_1\)に固定すると\(t_1\)の波形\(y(x,t_1)\)あるいは\(t_1\)での\(y\)-\(x\)グラフが扱える。 (☆2)
ところで(☆1)中の\(x_1\)は任意の\(x_1\)という意味だから、波の式\(y(x,t)\)は全ての位置\(x_1\)の\(y\)-\(t\)グラフを包含している。
(☆2)中の\(t_1\)は任意の\(t_1\)という意味だから、波の式\(y(x,t)\)は全ての時刻\(t_1\)の\(y\)-\(x\)グラフを包含している。
全ての\(y\)-\(t\)グラフ、\(y\)-\(x\)グラフを扱える、まさに波動を完全に記述する式が波の式である。


