10-03-1: 保存力

保存力・非保存力の本格的な説明をします。　→　関連事項は10-03-2: 位置エネルギー、10-04-1: 力学的エネルギー保存則の証明 へ　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

　このトピックでは重力が保存力であることを証明する。保存力とは、物体の始めの位置と終りの位置だけで仕事の値が決まってしまい、その値が途中の移動経路しだいで変わらない力である（図１）。

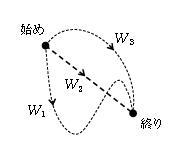
　これを証明するには、2次元の運動エネルギーと仕事の関係
　運動エネルギー変化 ＝　仕事　　　　を用いる。
　\(\displaystyle \frac{m}{2}|\vec{v}|^2- \frac{m}{2}|\vec{v_0}|^2 \) \(=\)　\(\displaystyle W=\lim_{\Delta \vec{r}→\vec{0}} \sum_{\Delta \vec{r}} |\vec{F}|\cos\phi \cdot |\Delta \vec{r}| \)
この式の導出・説明については1-16-2,1-16-3を参照してほしい。が、右辺の仕事\(W\)について手短かに説明すると ―― 右辺の中にある\(|\Delta \vec{r}| \)は微小な距離を表し、\(\phi\)は\(\vec{F}\)と\(\Delta \vec{r}\)(微小変位)のなす角、\(|\vec{F}|\cos\phi \)は力\(\vec{F}\)のうち物体の移動方向\(\Delta \vec{r}\)に沿う成分を表す。ゆえに\(W\)は「(力の移動方向成分)×(微小距離)を足し上げたもの」というような意味。以後これを
　\(W= \sum |\vec{F}|\cos\phi \cdot |\Delta \vec{r}| \; \)　　　　　　　　　　(1)
と略記する。\(\sum\)の後に来る\(|\vec{F}|\cos\phi \cdot |\Delta \vec{r}| \)は、(1)の\(W\)のうち\(\sum\)(和)を取らない部分で
　微小仕事\(\Delta W= |\vec{F}|\cos\phi \cdot |\Delta \vec{r}| \)　　　　　　　(2)
である。もちろん \(W=\sum\Delta W \;\: \)　　　　　　　　(3)

　早速、重力を受ける小球の2次元運動を考えよう（図２）。曲線は任意の軌道を表している（が、イメージ的にはジェットコースターに沿う軌道）。図の左側に下降中の\(\Delta r\)(\(=|\Delta \vec{r}| \))、右側に上昇中の\(\Delta r\)が示されている。重力\(mg\)と\(\Delta r\)の成す角が\(\phi\)だ。微小仕事\(\Delta W\)は(2)より
　\(\Delta W =mg\cos\phi \cdot \Delta r　\;\: \)　　　　　　　　　　(4)
　この式中の\(\cos\phi \cdot \Delta r\)に注目してみる。図２を見ると \(\cos\phi \cdot \Delta r =\Delta y\) となりそうだが、正しくは \(-\) \(\Delta y\)である。なぜなら ―― \(y\)軸上向きを正として、
　下降中は\(\Delta y<0\)、一方0°\(<\phi<\)90°より\(\cos\phi >0\)すなわち\(\cos\phi \cdot \Delta r >0\)
　上昇中は\(\Delta y>0\)、一方90°\(<\phi<\)180°より\(\cos\phi <0\)、\(\cos\phi \cdot \Delta r <0\)
つまり、下降中も上昇中も\(\Delta y\)と\(\cos\phi \cdot \Delta r\)は互いに逆符号だから、\(\cos\phi \cdot \Delta r =-\Delta y\) となるのである。したがって(4)は
　\(\Delta W= -mg\Delta y \)　これが任意の軌道の下降中・上昇中いずれも成り立つ重力の微小仕事で、(2)を重力について表した量である。すると(3)より
　\(W=\sum (-mg\Delta y)=-mg\sum \Delta y \, \)　　　　　 (5)
　この式中の\(\sum \Delta y \)だが、

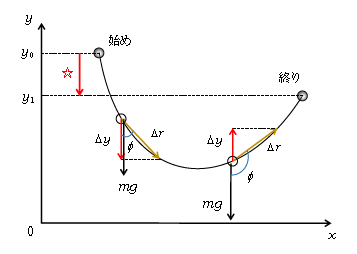
　図２を見ると \(\sum \Delta y =\) (\(y\)の変化量\(\Delta y\)の合計) \(=\)終りの\(y-\)始めの\(y=y_1-y_0\) 。これを(5)に代入して
　\(W= mg(y_0-y_1)\)　　　\(y_0-y_1\)は始めから終りの高さの減少分(図中の赤い☆)だから
　重力の仕事\(＝mg\)×(高さの減少分)
という重要な結論が得られた。ところで、高さの減少分は始めの位置と終りの位置だけで値が決まってしまい、その値が途中の移動経路しだいで変わらない（図１）。ということは、重力の仕事も始めと終りの位置だけで値が決まり、経路しだいで変わらない。よって、重力がこの単元冒頭の保存力であることが証明された。

　大学入試としては、保存力は重力、弾性力、万有引力、クーロン力の4つだけである。保存力については、10-03-2で扱う通り位置エネルギーが定義できる（たとえば重力による位置エネルギー）。一方、保存力以外の全ての力（摩擦力、張力、気体の圧力による力、…など）は非保存力といい、仕事の値が移動経路しだいで変わってくる力である。非保存力については位置エネルギーは定義できない（摩擦力による位置エネルギーなどない）。
　[ なお、ローレンツ力はつねに仕事が0という性質があり、定義によれば保存力に分類されるが、つねに仕事が0なので位置エネルギー（10-03-2の通り保存力がすることのできる仕事）を論ずることに意味がない。ゆえに、ローレンツ力を保存力として銘記しておくことに事実上意味はない。また、核力は原子物理で登場する力だが、ミクロな世界の軌道という概念は量子力学(大学の課程)的に問題をはらんでいる。ゆえに核力は保存力に含めなかった（とだけコメントし、これ以上深入りはしない）。]