1-45-3: ばねの両端 ー 片方から見た相対運動 #その1

ばね相互作用を違う切り口で捉えて理解を深めましょう！　→　＜続き＞は1-45-4へ　　　　　　　　　　　　

　この単元では、球1から見た球2の相対運動を扱う。「球1から見る」とは、球1の速度\(v_1\)で動く観測者(以後単に人と呼ぶ)から見るということ。ところでタクシーに乗っている人から見ると自分の足元は止まって見えるのと同様に、\(v_1\)で動く人から見ると足元の球1は止まって見える。つまり、球1を固定した上で、球2が相対的にどのような運動をするかを考えることにし、1-45-1,1-45-2の「重心から球1,2を見る」見方と対比していく。なお、球2から見た球1の相対運動は1-45-4で扱う。
　問題設定は1-44-1と同じで、図１に1-44-1の図１を再掲してある。 運動方程式は1-44-1の通り
　球1: \(m_1a_1=+f=+k(x_2-x_1-l)\)　　　　　 　　　　　(1)
　球2: \(m_2a_2=-f=-k(x_2-x_1-l)\)　　　　　 　　　　　(2)

　重心運動を扱うには(1)+(2)を\(m_1+m_2\)で割った(1-44-1)。球1から見た相対運動を扱うには、(2)÷\(m_2-\)(1)÷\(m_1\)とする。
　\(\displaystyle a_2-a_1=-\left(\frac{1}{m_2}+\frac{1}{m_1}\right)k(x_2-x_1-l)\)　　　　　　　(3)
ここで左辺は球1から見た球2の相対加速度である(「から見た」を引き算する公式(1-30-1)）。つまり、(2)(1)をそれぞれ\(m_2,m_1\)で割って左辺の\(a_2,a_1\)の係数を1に揃えて引くと、相対加速度が得られて相対運動が扱える。1-22-1の通り加速度\(a=\frac{d}{dt}v=\frac{d}{dt}\frac{d}{dt}x=\frac{d^2}{dt^2}x\)だから、
　(3)の左辺\(\displaystyle =\frac{d^2}{dt^2}x_2-\frac{d^2}{dt^2}x_1=\frac{d^2}{dt^2}(x_2-x_1)\)
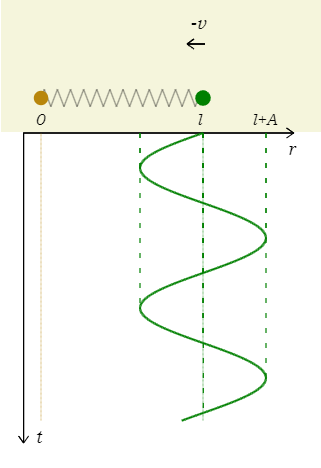
いま\(r=x_2-x_1\)とおくと、\(r\)は球1から見た球2の相対位置を表す。あるいは\(r\)は時刻\(t\)でのばねの長さとも言える。すると
　(3)の左辺\(\displaystyle =\frac{d^2r}{dt^2}\)
　ゆえに(3)は　\(\displaystyle \frac{d^2r}{dt^2}=-\left[\frac{1}{m_1}+\frac{1}{m_2}\right]k(r-l)\:\)　　　　　　(4)
　これは　変数\(r\)の2階微分\(=-\)〇(\(r-\)□) の形
だから、変数\(r\)の単振動の方程式である(1-24-1)。したがって、〇\(=\omega^2 \)、□\(=r_c\)(\(r\)の中心値)と読み取れ、\(r=A\sin(\omega t+\phi)+r_c\)と三角関数で表せる。そう、ばね相互作用では、ばねの長さ\(r\)は\(t\)の三角関数としてふるまうのだ。
　ここで、(4)の[　]の中身を\(\frac{1}{\mu}\)と表すのが通例である。すなわち
　\(\displaystyle \frac{1}{\mu}=\frac{1}{m_1}+\frac{1}{m_2}=\frac{m_2+m_1}{m_1m_2}\)　　∴　\(\displaystyle \mu=\frac{m_1m_2}{m_1+m_2}\;\)　 (5)
　\(\mu\)の分子の単位は[\(\text{kg}^2\)]、分母は[\(\text{kg}\)]だから、\(\mu\)の単位は[\(\text{kg}\)]、そのことに由来して\(\mu\)には「換算質量（reduced mass）」という名前が付いている。なお
　\(\displaystyle \frac{1}{\mu}=\frac{1}{m_1}+\frac{1}{m_2}>\frac{1}{m_1}\) より \(\mu<m_1\)　,　\(\displaystyle \frac{1}{\mu}=\frac{1}{m_1}+\frac{1}{m_2}>\frac{1}{m_2}\) より \(\mu<m_2\)　(5′)
つまり、\(\mu\)は\(m_1,m_2\)双方より減っている。そこでreduced(減少reductionの派生語）という名称が付いたものと思われる。結局(4)は
　　　　　　　　　　 \(\displaystyle \frac{d^2r}{dt^2}=-\frac{k}{\mu}(r-l)\)　
これを単振動の方程式 \(\displaystyle \frac{d^2r}{dt^2} =-\omega^2 (r-r_c) \)　と比べて、
　\(\displaystyle \omega=\sqrt{\frac{k}{\mu}}=\sqrt{\frac{k(m_1+m_2)}{m_1m_2}} \) [ (5)を代入した ] , \(r_c=l\;\)　 (6)　　と読み取れる。
　\(r_c=l\)より、ばね相互作用は自然長\(l\)を中心値としてばねの長さ\(r\)が長くなったり短くなったりすると分かる。　　
　また、周期\(\displaystyle T=\frac{2\pi}{\omega}\)(1-23-1)\(\displaystyle =2\pi \sqrt{\frac{\mu}{k}}\)　
　(5′)より \(\displaystyle T<2\pi \sqrt{\frac{m_1}{k}}\,,\,2\pi \sqrt{\frac{m_2}{k}}\) すなわち、2球がともに動くばね相互作用の周期は、一方の球だけが動くときの周期\(2\pi \sqrt{\frac{m_1}{k}}\,,\,2\pi \sqrt{\frac{m_2}{k}}\) に比べて短い。このことを理解するのに、重心から見る1-45-2では、重心の左(右)側のばねの方が全体のばねよりもばね定数が強くなるという捉え方をした。が、球1から見るこの単元では、換算質量\(\mu\)が\(m_1,m_2\)より小さいとして理解できる（抽象的ではあるが）。

　それでは、1-45-1のように (\(t=0\)での値に＊を付けて)\(x^*_1=0\),\(x^*_2=l\), \(v^*_1=v>0\),\(v^*_2=0\)かつ\(m_1=m,m_2=2m\)の場合を具体的に扱おう。このとき(6)より
　\(\displaystyle \omega=\sqrt{\frac{k(m+2m)}{m\cdot2m}}=\sqrt{\frac{3k}{2m}} \) , \(r_c\) \(=l\:\,\)　　　　　　　　　(6′)
　周期\(\displaystyle T=\frac{2\pi}{\omega}=2\pi \sqrt{\frac{2m}{3k}}\)　これは1-45-2の\(T\)と一致する。
　いま、ばねの長さの初期値\(r^*=x^*_2-x^*_1=l\)、相対初速度\(u^*=v^*_2-v^*_1=-v\)
　これはつり合い点(自然長\(l\))で初速度\(-v\)を与えるパターン(1-24-2)だから、図２のような-sin型のグラフになる（\(t\)軸を下向きに取った）。これを1-45-2の図２(再掲)と比べると印象深いだろう。振幅\(A\)を求めるには、公式「つり合い点にて\(v_{\text{max}} =A\omega\)」(1-24-2)より
　\(|u^*|=A{\omega}\)　　∴　\(\displaystyle A=\frac{v}{\omega}=v\sqrt{\frac{2m}{3k}}\)　[ (6′)を代入した ]　これは1-45-2のばね全体の振幅\(A\)と一致する。\(r\)を\(t\)の関数で表すと　
　\(\displaystyle r=-A\sin\omega t+r_c=-v\sqrt{\frac{2m}{3k}}\sin\sqrt{\frac{3k}{2m}}t+l\:\)　　　 　(7)

　入試では、1-45-1,1-45-2のように重心から見る文脈で出題される場合と、この単元のように片方の球から見る出題がある。重心から見る出題ならまさに重心から見ればよいし、片方の球から見る出題なら片方の球から見るのがよい。
　次の単元1-45-4では、発展的内容を一つ追加した後に、球2から見た球1の相対運動を扱う。