1-31-2: 運動量保存則 <例題1>(1次元衝突)
入試で頻出の1次元衝突を是非マスターしましょう! → 1-31-3<例題2>へ続く
例題1
図のように、水平で滑らかな床の上を紙面内で運動または静止する2つの小球A(質量\(m\))、B(質量\(M\))について考える。いま、静止しているBにAが速さ\(v_0\)で衝突した。衝突のはね返り係数\(e\)をとし、また右向きを正の向きとする。
問1 衝突後のA、Bの速度を求めよ。
問2 (i) \(m<<M \) (ii) \(m>>M \) (iii) \(m=M\) の各場合について、\(e=1\)のときA、Bの速度はいくらになるか答えよ。
[ << (>>) は「ひじょうに小さい(大きい)」という意味の記号。つまり \(m<<M \)は 「\(m\) は\(M\)に比べると無視できるほどにひじょうに小さい」ということである ]
問3 AがBから受ける力積を求めよ。
解答・解説
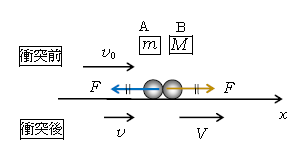
図1のように衝突後のA、Bの速度をそれぞれ\(v,\,V \)とおく。速度は正の向きに図示してあるが、たとえば求まった\(v\)が負ならば、衝突後Aは負の向きに動くという意味。
問1 1次元衝突を調べる上での主たる目的は、衝突後の2物体の速度を求めることである。ゆえに式が2つ必要。1-31-1でやった通り、1次元衝突では運動量保存則が成り立つ。これとはね返り係数の式を連立すればよい。
あと まえ
図1より、運動量保存 \(mv+MV=mv_0+M0 \) (1)
はね返り係数の式 \(v-V=-e(v_0-0) \) (2)
(2)より \(V=v+ev_0 \, \) (3)
(1)に代入 \(mv+M(v+ev_0)=mv_0 \) \(∴ (m+M)v=(m-eM)v_0 \)
\(\displaystyle ∴ v=\frac{m-eM}{m+M}v_0 \)
(3)より \(\displaystyle V=\frac{m-eM + e(m+M)}{m+M} \; v_0 =\frac{(1+e)m}{m+M}v_0 \)
答 A: \(\displaystyle \frac{m-eM}{m+M}v_0 \) B: \(\displaystyle \frac{(1+e)m}{m+M}v_0\)
問2 \(e=1\)のとき \(\displaystyle v=\frac{m-M}{m+M}v_0 \) 、\(\displaystyle V=\frac{2m}{m+M}v_0 \)
(i) \(m<<M \)により \(\displaystyle v≒\frac{0-M}{0+M}v_0 =-v_0 \) 、\(\displaystyle V≒\frac{0}{0+M}v_0 =0 \)
答 A: \(-v_0\) B: \(0\)
[ いま\(m<<M \)ということは、Bがずっしり重いレンガ、Aが軽いピンポン玉のようにイメージできる。するとBは衝突後止まったままであることが容易に想像できる。また、はね返り係数1(100%)だから、Bから見たAの衝突前の相対速度\(v_0-0=v_0\)に対し、衝突後の相対速度が\(-1×(v_0-0)=-v_0 \)になる ]
[ このように、レンガ、ピンポン玉のような極端な状況をイメージするのがコツ ]
(ii) \(m>>M \)の場合の計算は次のようにやる。分母分子を\(m\)で割って、\(\frac{M}{m}\)がほぼ0であることに注意すると、
\(\displaystyle v=\frac{1-\frac{M}{m}}{1+\frac{M}{m}}v_0 ≒ \frac{1-0}{1+0}v_0=v_0 \) 、\( \displaystyle V=\frac{2}{1+\frac{M}{m}}v_0 ≒ \frac{2}{1+0}v_0=2v_0 \)
答 A: \(v_0\) B: \(2v_0\)
[ \(m>>M \)なので、Aがずっしり重いボーリング玉、Bが軽いピンポン玉のようにイメージできる。するとAは衝突後速度を変えず\(v_0\)のままであることが容易に想像できる。また、はね返り係数1だから、Bから見たAの衝突前の相対速度\(v_0\)に対し、衝突後の相対速度が\(v_0-2v_0=-v_0 \)になる ]
(iii) \(m=M \)により \(\displaystyle v=\frac{m-m}{m+m}v_0 =0 \) 、 \(\displaystyle V=\frac{2m}{m+m}v_0 =v_0\)
答 A: \(0\) B: \(v_0\)
[ A,Bの衝突前の速度がそれぞれ\(v_0,\,0 \)なのに対し、衝突後はそれぞれ\(0,\,v_0 \)になったということは、速度がAとBで入れ替わっている(\(v_0,\,0 \)から\(0,\,v_0 \)に)。これを、「2球の1次元弾性衝突(\(e=1\))では速度が交換する」という。A,Bの衝突前の速度がたとえば\(3v_0,\,v_0 \)なら\(v_0,\,3v_0 \)に交換する、など。この結果は覚えておくと便利である ]
問3 Aの受けた力積=「Aの」運動量変化(図1より)\(=mv-mv_0\)
\(\displaystyle =m(v-v_0)=m\left( \frac{m-eM}{m+M}v_0 -v_0 \right) \)
\(\displaystyle =m\frac{m-eM -(m+M)}{m+M} \: v_0 \)
∴ 答 \(\displaystyle -\frac{(1+e)mM}{m+M}v_0 \)
[ AはBから左向きの\(F\)で押される(図1)から、当然その力積は負である ]


