1-15-3: 放物運動のグラフによる考察

話を等加速度直線運動の対称性にまで広げます。　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

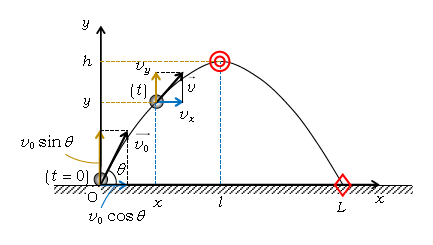
　図１は1-15-2の図の再掲。
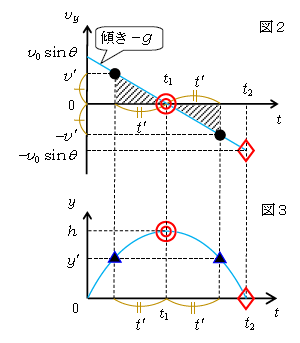
　図２は1-15-2で求めた\(v_y=v_0\sin\theta -gt \) を縦軸\(v_y\) 、横軸\(t\)のグラフにしたもの。\(t\)の１次関数だから直線のグラフで、\(v_y\)-\(t\)グラフの傾き\(＝a_y\)\(=-g\) に注意する。最高点(◎印)に達する時刻は1-15-2で\(\displaystyle t_1=\frac{v_0}{g}\sin\theta \)、落下点(◇印)の時刻は\(\displaystyle t_2=\frac{2v_0}{g}\sin\theta \)だった。このうち\(t_1\)については、グラフの傾き\(\displaystyle g=\frac{タテv_0\sin\theta}{ヨコt_1} \) から\(\displaystyle t_1=\frac{v_0}{g}\sin\theta \) と求めることもできる。
　図３は1-15-2の\(\displaystyle y=v_0\sin\theta \cdot t -\frac{1}{2}gt^2\) を縦軸\(y\)、横軸\(t\)に取ったグラフで\(t\)の２次関数。平方完成すると\(\displaystyle\)
　　\(\displaystyle \)\(\displaystyle y=-\frac{1}{2}g \left( t^2-\frac{2v_0}{g}\sin\theta \cdot t \right)=-\frac{1}{2}g \left(t-\frac{v_0}{g}\sin\theta \right)^2+\frac{v_0^2}{2g}\sin^2\theta \)
　となって、軸\(\displaystyle t=\frac{v_0}{g}\sin\theta=t_1 \)、頂点の\(\displaystyle y=\frac{v_0^2}{2g}\sin^2\theta \) 。頂点は1-15-2の\(h\)と等しいことが分かる。

　このようにグラフを書いてみると以下のことが言える。
　２次関数のグラフは軸に関して線対称だから、\(t_2=2t_1\)（図３）。つまり上昇時間と下降時間は等しい。
　すると、図２で横軸\(0～t_1\)を底辺に持つ直角三角形と\(t_1～t_2\)を底辺とする直角三角形の底辺どうしが等しいから、高さどうしも等しく、初速度\(v_0\sin\theta \)に対して落下点での速度\(-v_0\sin\theta \)となる。つまり上昇速度と下降速度は互いに(-1)倍である。

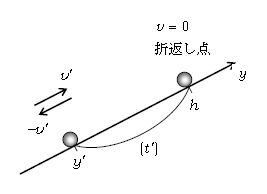
　今述べたこを広く一般化しよう。実は鉛直方向に限らず、水平方向だろうが斜面方向だろうが、等加速度直線運動でUターンする地点「折返し点」が絡む場合は、必ず図２のように\(v\)-\(t\)グラフは右下がりの直線になる。というのも、縦軸の\(v\)が正(正の向きへの運動)からやがて負(負の向きへの運動)に切り替わるとUターンするからで、このとき\(v=０\)の所（◎印）が折返し点になる。\(v\)-\(t\)グラフの面積は変位を表すから（1-02-1)、図２の斜線の面積が等しい所は、図３では◎印の折返し点までの距離が等しい2地点（▲印）に対応する。斜線を施した２つの直角三角形は面積が等しく対頂角も等しいから合同で、底辺どうしが等しい。すると、◎の折り返し点までにかかる時間と折返し点からかかる時間はともに\(t’\)で等しい。
　また、斜線を施した２つの直角三角形は高さどうしが等しいから、速さどうしも等しい（図２の●印）。
　以上を等加速度直線運動の対称性（時間の対称性、速さの対称性）という。便利だからぜひ覚えておこう。一例を図４に示した。