1-12-2: 浮力 ＜例題＞

例題を一挙に２つ練習しましょう！　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

例題１

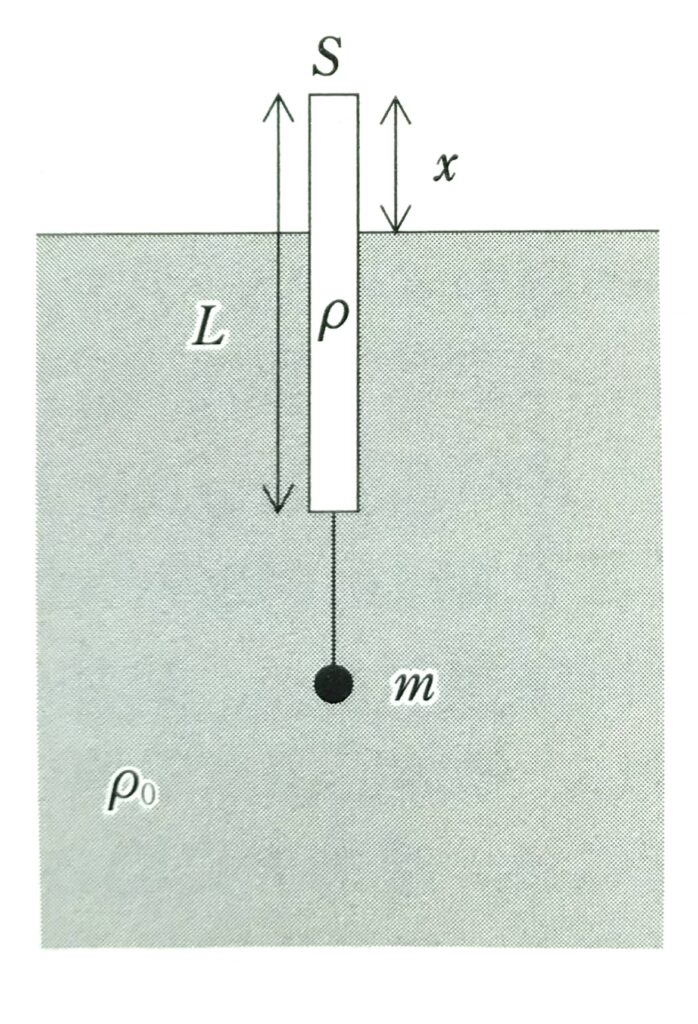
　図のように、浮きを水面に垂直に浮かべた。浮きは断面積\(S\)、長さ\(L\)の細長い一様な円柱であり、その下には質量\(m\)のおもりが糸でつり下げられている。水の密度を\(\rho_0\)、浮きの密度を\(\rho\)（\(\rho <\rho_0 \)）とする。浮きが上端を水面上に出して静止しているとき、上端の水面からの高さ\(x\)として正しいものを、次の①～⑧のうちから一つ選べ。ただし、糸の質量と太さおよびおもりの大きさは無視できるものとする。
①　\(\displaystyle \left( 1-\frac{\rho}{\rho_0} \right) L+\frac{m}{\rho S} \)　　②　\(\displaystyle \left( 1-\frac{\rho}{\rho_0} \right) L-\frac{m}{\rho S} \)　　
③　\(\displaystyle \left( 1+\frac{\rho}{\rho_0} \right) L+\frac{m}{\rho S} \)　　④　\(\displaystyle \left( 1+\frac{\rho}{\rho_0} \right) L-\frac{m}{\rho S} \)　　
⑤　\(\displaystyle \left( 1-\frac{\rho}{\rho_0} \right) L+\frac{m}{\rho_0 S} \)　　⑥　\(\displaystyle \left( 1-\frac{\rho}{\rho_0} \right) L-\frac{m}{\rho_0 S} \)　　
⑦　\(\displaystyle \left( 1+\frac{\rho}{\rho_0} \right) L+\frac{m}{\rho_0 S} \)　　⑧　\(\displaystyle \left( 1+\frac{\rho}{\rho_0} \right) L-\frac{m}{\rho_0 S} \)

解答・解説

　1-08-1: 力学攻略の基本　の流れに従って行く。
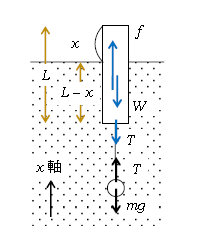
　まず軸と力（図１）。
　浮きに働く重力\(W=m_{うき}g=\rho_{うき} V_{うき} g=\rho SLg \)
　(1)式より、浮きに働く浮力\(f=\rho_水 V_下 g=\rho_0 S(L-x)g \)　などに注意する。

　
　次に\(ma=F\)　（つり合いの式）
　浮き　　\(0=\rho_0 S(L-x)g -\rho SLg -T \)　 (2)
　おもり　\(0=T-mg \, \)　　　　　　　　　　　(3)
　(2)+(3)で\(T\)を消去　\(0=\rho_0 S(L-x)g -\rho SLg -mg \)
　\(\rho_0 Sg \)で割って　\(\displaystyle 0=L-x-\frac{\rho}{\rho_0} L-\frac{m}{\rho_0 S} \) 
　　∴　\(\displaystyle x=\left(1-\frac{\rho}{\rho_0} \right) L-\frac{m}{\rho_0 S} \)　　　　答　⑥

例題２　

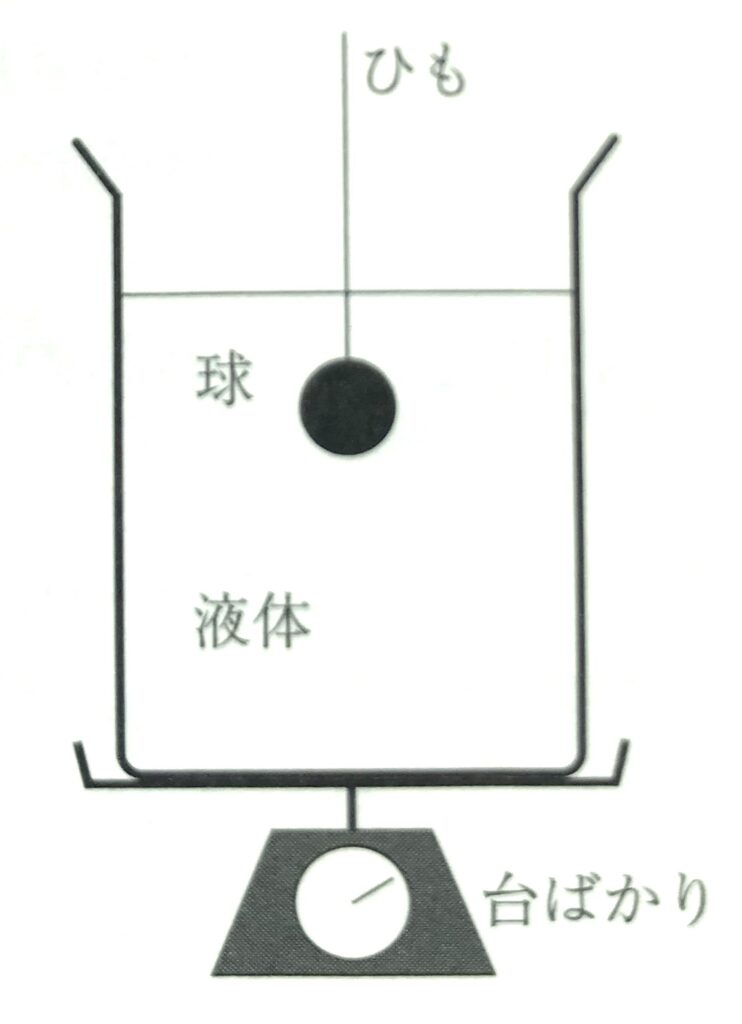
　密度\(\rho\)、体積\(V\)の液体を入れた容器が、台ばかりにのっている。図のように、密度\({\rho}’ \)、体積\(V’\)の球（\({\rho}’>\rho \)）を細いひもで上からつって、液体中で静止させた。このとき、はかりが示す力の大きさはいくらか。正しいものを、次の①～⑥のうちから一つ選べ。ただし、容器の質量は無視できるものとし、重力加速度の大きさを\(g\)とする。
①　\({\rho}’ Vg \)　　②　\({\rho}'(V+V’)g \)　　③　\((\rho V +{\rho}’V’)g \)　　
④　\(\rho Vg \)　　⑤　\(\rho (V+V’)g \)　　⑥　\(({\rho}’ V+\rho V’)g \)　

解答・解説

　この問題は、はかり、球、容器＋水(を1物体と見なしたもの)、などいろいろと注目物体がありそうだし、しかもそれらがふれ合っている。1-10-1でやった通り、注目物体どうしがふれ合っている所での作用反作用に注意。まずはそれを押さえよう。
　図２ではかりが容器＋水を\(N\)で押すということは、作用反作用により、容器＋水ははかりを\(N\)で押している。この\(N\)の大小で、はかりの針のふれの大小も決まる。つまり、問題文中の「はかりが示す力の大きさ」とは、容器＋水からはかりに加わる\(N\)のことである。

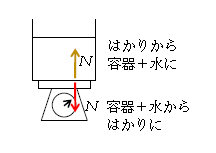
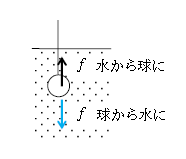
　一方、水から球に浮力\(f\)（水圧による合力）が働く（図３）ということは、球から水に下向きに浮力の反作用\(f\)が加わる。　

　さて、\(N\)を求めたいので、注目物体を容器＋水にしてつり合いから求めるのがよい（図４）（注目物体をはかりに取っても計算は進まない）。　　[ 自分が注目物体を何に取っているのかを、常に意識しよう。注目物体を何に取ればよいか見抜くには、ある程度練習を積む必要がある。]

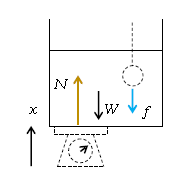
　まず軸と力　「容器の質量は無視」とあるから、
　　重力\(W=m_水 g=\rho _水 V_水 g=\rho Vg \)
　(1)より、浮力の反作用\(f=\rho _水 V_下 g=\rho V’g \)
　次に\(ma=F\)　　\(0=N-\rho Vg -\rho V’g \)    
　　∴　\(N=\rho (V+V’)g \)　　　　答　⑤