10-02-3: 力には向きがある、仕事には向きがない #その３

お疲れさま、さあ、あと一息です！　→　＜#その1＞は10-02-1、＜#その2＞は10-02-2へ　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

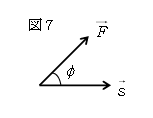
　いよいよ「仕事」を考えよう。仕事の厳密な定義には数学の積分を必要とするが、本質がつかめればそれでよいから、簡単化した定義から始めることにする。物体に加わる力\(\vec{F}\)と物体の変位\(\vec{s}\)を用いて
　仕事 \(W=\vec{F} \cdot \vec{s} \)
と定義される（図７）。もちろん「\(\cdot \)」(ドット)はベクトルの内積であり、従って\(W=F_x s_x +F_y s_y \tag{3} \)とも書けるし、\(W=|\vec{F}||\vec{s}|\cos\phi \tag{4} \)とも書ける。

 　仕事が回転変換に対してどのようにふるまうかを見よう。(☆)と同様にして
\begin{equation} \begin{cases}
{F_x}’=F_x\cos\theta +F_y\sin\theta \\
{F_y}’=-F_x\sin\theta +F_y\cos\theta
\end{cases} \end{equation} \begin{equation} \begin{cases}
{s_x}’=s_x\cos\theta +s_y\sin\theta \\
{s_y}’=-s_x\sin\theta +s_y\cos\theta
\end{cases} \end{equation}　そこで\(x\)-\(y\)平面における仕事\(W’\)は、(3)より
　\(W’={F_x}'{ s_x}’ +{F_y}'{s_y}’ \)
　　\(=(F_x\cos\theta +F_y\sin\theta) (s_x\cos\theta +s_y\sin\theta) \)
　　　\(+(-F_x\sin\theta +F_y\cos\theta) (-s_x\sin\theta +s_y\cos\theta) \)
　　\(=F_x s_x (\cos^2\theta+\sin^2\theta) +F_xs_y (\cos\theta \sin\theta-\sin\theta \cos\theta) \)
　　　\(+F_ys_x (\sin\theta \cos\theta -\cos\theta \sin\theta) +F_y s_y (cos^2\theta+\sin^2\theta) \)
　　\(=F_x s_x +F_y s_y =W \)
　∴　　\(W’=W \)
　よって仕事は回転変換に際して不変である。すなわち仕事はスカラーであり、正負の符号はあっても向きはない。仕事に向きがないとは、まさにそういうことだったのである。それは温度がスカラーで向きがないのと全く同じである。
　仕事が回転変換に際して不変であることは、(4)を見るとよりはっきりするだろう。なぜなら\(|\vec{F}|, |\vec{s}|, \phi \)いずれも座標軸を回しても変化することのない量だからである。なお、以上の仕事がスカラーであることの証明は、広く一般に内積がスカラーであることの証明に他ならない。従って内積で書ける他の物理量（例えば電磁気学に出てくる磁束\(\Phi \)）についても当てはまる。

物理法則の共変性

　普段物理を学習していて、次のようなことを思ったことはないだろうか。すなわち、高校物理で学ぶ法則には、不思議とベクトル式かスカラー式しか出てこない。例えば運動方程式
　\(m\vec{a}=\vec{F} \)
はベクトル式であり、力学的エネルギー保存則
　\(\frac{1}{2} m{v_1}^2 +mgh_1 =\frac{1}{2} m{v_2}^2 +mgh_2 \)
はスカラー式である。そこで最後に、物理法則がベクトル式やスカラー式で書けることの意義を考えていくことにしよう。

　ある物理現象（例えば小球の飛行）を観測者Aが座標軸\(x\)-\(y\)で記述してその運動方程式を\( ma_x=F_x, \quad ma_y=F_y \tag{5} \)と書いたとしよう。一方観測者A’ が座標軸\(x’\)-\(y’\)を用いて\(m{a_x}’={F_x}’, \quad m{a_y}’={F_y}’ \tag{6} \)と書いたとする。２人の書いた式の関係はどうなっているだろうか。規則(☆)より
\begin{equation} \begin{cases}
{a_x}’=a_x\cos\theta +a_y\sin\theta \\
{a_y}’=-a_x\sin\theta +a_y\cos\theta
\end{cases} \end{equation} \begin{equation} \begin{cases}
{F_x}’=F_x\cos\theta +F_y\sin\theta \\
{F_y}’=-F_x\sin\theta +F_y\cos\theta
\end{cases} \end{equation} 　これらを(6)に代入すると、\(m(a_x\cos\theta +a_y\sin\theta) =F_x\cos\theta +F_y\sin\theta \tag{7} \) \(m(-a_x\sin\theta +a_y\cos\theta) =-F_x\sin\theta +F_y\cos\theta \tag{8} \)　(7)×\(\cos\theta \)+(8)×\((-\sin\theta) \)を計算してみると
　　\(ma_x (\cos^2\theta +\sin^2\theta)=F_x (\cos^2\theta +\sin^2\theta) \)　　
　　∴　\( ma_x=F_x \)
　(7)×\(\sin\theta \)+(8)×\(\cos\theta \)は
　　\(ma_y (\sin^2\theta +\cos^2\theta)=F_y (\sin^2\theta +\cos^2\theta) \)　　
　　∴　\( ma_y=F_y \)
　従って(6)から(5)が得られた。同様にして(5)から(6)が得られるので、(5)と(6)は全く同値であることが分かる。つまり２人の観測者の書く運動方程式は一見異なるように見えても（例えば10-02-1の(I)と(II)がそうだった）、それらは同値であり、全く同じ内容を表していることになる（例えば10-02-1の落下時間(1)と(2)は一致した）。もっと広く一般化するならば、ベクトル式で書かれた物理法則は、回転変換によってその成分表示を変えはするが、同値関係は保ちその意味内容を変えない。言うまでもなく、人間がどう座標軸を取ろうと取るまいと、自然界の物理現象は一定の規則性に従って厳然と起こるのであり、その法則性の変わるはずもなかろう。つまり物理法則がベクトル式で表現されるとき、そこには物理現象が座標軸の取り方に左右されることのない法則性の下整然と営まれるという雄弁な主張が込められているのである。例えばベクトル式の運動方程式\(m\vec{a}=\vec{F} \)は、座標軸をどう取ろうとも、ともかく力が加わればその向きに加速度が生じるという現象の起こることを積極的に主張している。
　またスカラー量は回転変換に際して不変であるから、物理法則がスカラー式で表現された場合にも回転変換に対して同値性が保たれることは明白である。
　物理法則が座標軸の回転に対して(5)と(6)のような同じ形式を保ち同値関係を保つことを、物理法則は回転変換に関して「共変」であるという。こう考えてくると、一般に物理法則は、回転変換に関して共変なベクトル式かスカラー式のいずれかで書かれるべきである、といったことが結論されそうである。高校物理の範囲内ではそれは全く正しい。ただし大学に行くと、諸君はテンソルやスピノールといった新たな共変形式を学ぶことになるだろうし、回転変換の相対論的拡張としてのローレンツ変換も学ぶだろう。楽しみにしていてほしい。

　最後に予備校講師目線としてのアドバイスを１つ。問題を解くとき座標軸をどう取ったらよいのか大いに迷ってしまう学生をしばしば見受ける。座標軸の取り方によっては不正解になるのではないかという不安もあるのだろう。しかし心配無用。物理法則は共変なのであるから、どのように座標軸を取っても正解に達する。物理法則の共変性を信頼してほしい。要は自分が計算しやすいように自分の好きな座標軸を取ればよい。