2-12-2: 気柱の固有振動 <例題>
気柱の問題も弦の問題も、本質的な考え方は変わりません。 → 気柱の固有振動 の説明は2-12-1へ
※ 2-12-1で扱った共鳴とは ―― 気柱に音を送り込んだとき気柱から音が強く聞こえてくる現象。このとき気柱には送り込んだ音と等しい振動数を持つ固有振動が生じている。
例題
任意の振動数の音波を発生できるスピーカーSを、両端の開いたガラス管の左側に置いた。
問1 振動数を0から次第にあげていくと、ある振動数のところで初めて共鳴した。このときの管内の空気振動のようすはどのような図で表わされるか。次の図①~④のうちから正しいものを選べ。ただし、開口端の補正は無視できるとし、図では空気振動の左右方向の変位を、上下方向の変位として表してある。
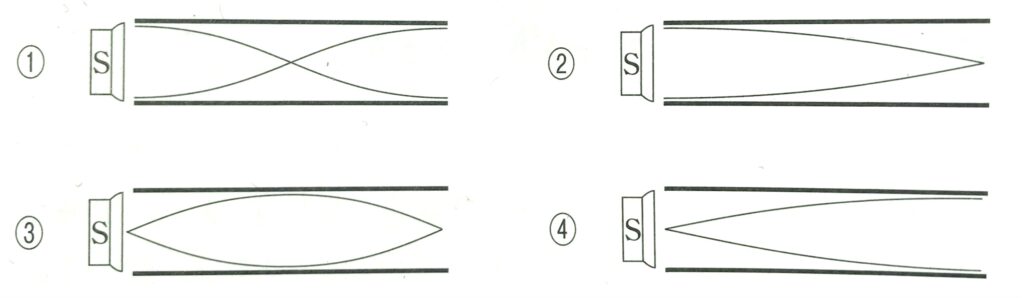
問2 振動数をさらにあげていくと、再びある振動数で共鳴した。このときの振動数は最初に共鳴したときの振動数の何倍か。最も適当な数値を、次の①~⑥のうちから1つ選べ。
① \(\displaystyle \frac{1}{2} \) ② \(1 \) ③ \(\displaystyle \frac{3}{2} \) ④ \(2 \) ⑤ \(\displaystyle \frac{5}{2} \) ⑥ \(3 \)
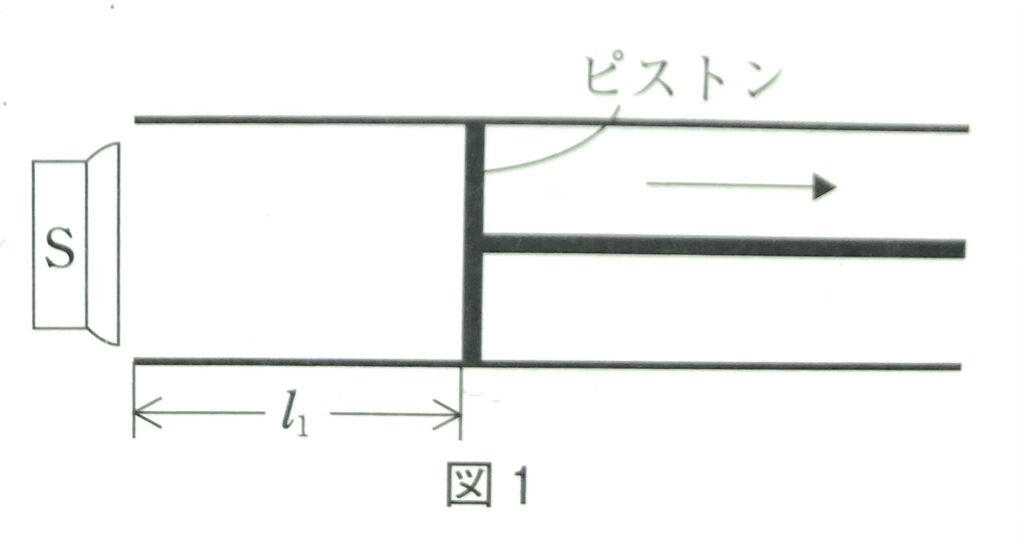
問3 次に、図1のようにガラス管の右端からピストンを入れて、振動数500Hzの音を出した。ピストンを左側の管口の位置からゆっくりと引き抜いていくと、管口から\(l_1\)の位置ではじめて共鳴した。さらに引き抜いていくと、管口から\(l_2\)の位置で再び共鳴した。\(l_2-l_1\)の値はいくらか。最も適当な数値を、次の①~⑥のうちから1つ選べ。ただし、音速は340m/sとする。
① 0.17 ② 0.34 ③ 0.51 ④ 0.68 ⑤ 0.85 ⑥ 1.36
解答・解説
問1 両開きのガラス管だから、閉管ではなく開管で、両端が腹
答 ①
問2 [ 固有振動は\(V,\lambda ,f\)を押さえる。\(V\)は音速 ]
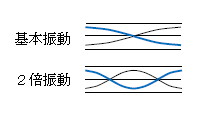
最初の共鳴は基本振動(図2)で、波の数\(\frac{1}{4} ×2=\frac{1}{2} \)だから
\(\displaystyle \lambda=\frac{l}{波の数}=\frac{l}{\frac{1}{2} } =2l \)
\(\displaystyle f=\frac{V}{\lambda} =\frac{V}{2l} \) (1)
次の共鳴は2倍振動で波の数\(\frac{1}{4} ×4=1 \)。
\(\displaystyle \lambda ' =\frac{l}{1} =l \) 、 \(\displaystyle f’=\frac{V}{\lambda '} =\frac{V}{l} \) (2)
(1)、(2)比べて \(f’=2×f \) 答 ④
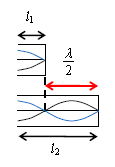
問3 今度は閉管で、最初の共鳴と、次の共鳴の様子は図3の通り。すると、\(\displaystyle l_2-l_1=\frac{\lambda}{2}\)であることが分かる。よって
\(\displaystyle l_2-l_1=\frac{V}{2f}=\frac{340 \, \text{m/s}}{2×500 \, \text{Hz}} =0.34\text{m} \) 答 ②