2-01-1: 波動分野の準備 ＜動画あり＞

波動の基本用語、基本公式からスタートしましょう！　　　　　　　　　　　　　　　　　　　　　　　　　　

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

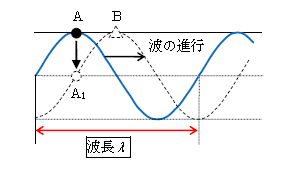
　ひもの正弦波（サインカーブの形をした波）が伝わるとき、サインカーブが形を保ったまま平行移動していく。波動とは、一定の波形が平行移動していく現象だ（図１）。波１個分（サインカーブ１個分）の長さを波長\(\lambda \)[m]という。 波を伝えていく物質（この場合はひも）を媒質といい、媒質の各点各点は媒質粒子から成る。
　このとき、粒子はA→Bと波とともに動くのではなく、A→A₁と上下方向に動く。

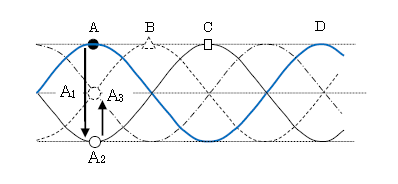
　時間が経つにつれて波形が図２の太線→点線→細線→鎖線のように平行移動していくと、粒子はA→A₁→A₂→A₃のように単振動をする。単振動とは、1-23-1の図2にあるような往復運動だ（動画は1-24-2を参照のこと）。波動では、単振動を略して振動と呼ぶことが多い。
　Aのように最も高い位置を 山 、A₂のように最も低い位置を 谷 、A₁、A₃を(振動)中心という。図２より、まずAが山になってから(太線)、少し遅れてBが山になり(点線)、さらに少し遅れてCが山になる(細線)ことが分かる。
　\(\displaystyle \)ところで、スポーツ観戦している観客が応援でウェーブ（波）を起こすときは ―― まず１列目の観客が立ち上がり、少し遅れて隣りの２列目の観客が立ち上がり、さらに少し遅れて３列目･･･というように、観客の立ち上がるタイミングが少しずつ遅れていくと、我々の目にはウェーブが平行移動していくのが見える。このとき、観客自体はウェーブとともに遠くへ遠くへ移動して行かない。ただその場で立ったり座ったりを繰り返すだけだ。

　これと同様に、波動とは、１点（A）の振動が少しずつ遅れたタイミングで隣りの隣りの（B、C、･･･）振動を引き起こしながら、波形(サインカーブ)が平行移動していく現象である。言い換えると波動では、粒子であれば中心のまわりに上下に振動する（2-04-1の縦波では左右に振動する）場合を扱う。粒子は遠くへ遠くへ移動しない。なお、振動を引き起こす（結果として波形が平行移動する）原因は、ひもを伝わる波では粒子どうしが引張り合う張力である。
　A→･･･→Aと元に戻るまでを振動１回といい、振動１回にかかる時間を周期\(T\)という。1sあたりの振動回数を振動数\(f\)という。
　振動数\(f\)は周期\(T\)の逆数だ :　\(\displaystyle f=\frac{1}{T} \)　[1/s=Hz]（ヘルツという）
　なぜ逆数なのかは、周期\(T\)を1sより短くイメージするとよく分かる。例えば振動１回にかかる時間(周期\(T\))が0.1sなら、1sあたりの振動回数(振動数\(f\)）はいくらだろう。確かに\(\frac{1}{0.1} \)=10回。

　さて、図２で粒子がA(太線)→A₁(点線)→A₂(細線)→A₃(1点鎖線)→Aと１回振動して元のAに戻ると、波形はA→B→C→Dと１波長進んで元のAを通る太線の波形になる。言いかえると、波は１周期\(T\)の間に１波長\(\lambda \)進む。\(\frac{1}{4}T\)なら\(\frac{1}{4} \lambda \)進む。速さは距離÷時間だから、波の進む速さ\(V\)=波長\(\lambda \)÷周期\(T\)、つまり
　波の速さ　\(\: V\)　=　\(\displaystyle \frac{\lambda}{T} \)　=　\(\lambda f \)　
　　　　　[\(\displaystyle \text{m}/\text{s} \)] = [\(\displaystyle \frac{\text{m}}{\text{s}} \)] = [\(\displaystyle \text{m} \frac{1}{\text{s}}\)]　
　この公式の覚え方は、まさに「１周期\(T\)で１波長\(\lambda \)進む」。さらに単位を付けながら覚えておけば、間違いがない。

　最後に動画をお見せしよう。