1-33-1: 束縛条件(垂直抗力に伴う条件)
束縛条件という難しく聞こえる用語に惑わされずに、入試の頻出問題をマスターしましょう! → <続き>は1-33-2へ、束縛条件(張力に伴う条件) は1-34-1へ
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント
・ 物体の接触している面から垂直抗力\(N\)が働く場合、
物体はその面から離れずに運動している。それを加速度の条件式として表せる。
1-32-1の2体問題で、斜面の形状が曲面ではなく、平面の場合を考えよう(図1。矢印の説明はこの後すぐ。なめらかで水平な床上を三角台が動ける状況。斜面もなめらかとする)。この場合も運動量保存と力学的エネルギー保存の連立の考え方はもちろん通用する。が、それだけではなく、1-08-1:力学攻略の基本 の流れ「まず軸と力 次に\(ma=F\) 運動\(v,x\)を調べる」も通用し、とりわけ「\(v,x\)を\(t\)の関数で表す」ことが可能である。そう、2物体の運動の時間的変化が調べられるのだ。これを見ていくことにしよう。
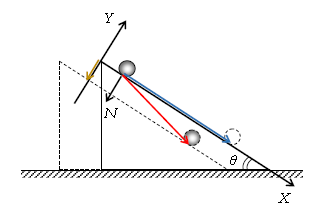
まず軸と力(図2)。なぜ水平右向きに\(x\)軸、鉛直上向きに\(y\)軸を取り、斜面に平行に\(x\)軸を取らなかったのか。図1に戻って ―― 小球(以後球と呼ぶ)から台に働く斜め左向きの\(N\)を受けて、台が左向きに実線から点線へと動く様子が示してある。対応して球も実線から点線へ赤い矢印のように動く。すると、斜面に平行に\(X\)軸、垂直に\(Y\)軸を取ると、球の\(Y\)座標が黄色い矢印のように加速することが分かる。ゆえに運動方程式の\(Y\)成分は\(ma_Y=\cdots \) のようになり、\(0=N-mg\cos\theta \) のようなつり合いの式にならない。[ 仮にこの台が固定台なら、球は青い矢印のように動いて球の\(Y\)座標は動かないから、つり合いになる。この問題を解くとき\(0=N-mg\cos\theta \)であると早合点してしまう学生がいるが、たった今説明した通り(また後で答を求めてみれば分かる通り)\(N=mg\cos\theta \)ではない ] 。したがって\(X,Y\)軸で考えるメリットはない。また、赤い矢印の向きの角度は\(\theta\)ではなく、何度になるのかも解いてみないと分からない。球の動き方は不明である。一方、台が\(-x\)方向(左向き)に動くことは確定している。ならば、台に合わせて\(x,y\)軸で考えようというわけである。
また、図2で加速度の成分は全て正の向きに\(a_x,a_y,A\)とおいた(図示した)。例えば\(A=-\)3のように負の値で求まったなら、実際は負の向きに加速するという意味である。決して右向きに加速中という意味ではない。
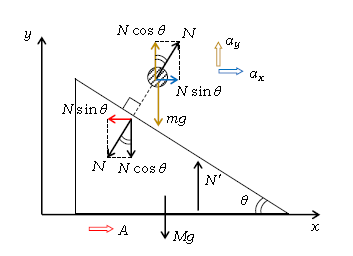
次に\(ma=F\) \(x,y\)軸に対して斜めの力\(N\)を分解する。\(y\)軸平行な\(mg\)は分解しない。
球: \(x\)成分 \(ma_x=N\sin\theta \) (1)
\(\;\)\(y\)成分 \(ma_y=N\cos\theta-mg \:\; \) (2)
台: \(x\)成分 \(MA=-N\sin\theta \) (3)
\(\;\)\(y\)成分 \(0=N’-N\cos\theta-Mg \)
式番号(4)を付けなかったのは、Bの\(y\)成分からは\(N’\)が求まるが、この式を後々使わないからである。なお1-15-1で述べた通り、加速度を図示しないまま\(ma_x=\cdots \) と立てるのも一法である。
さて、(1)(2)(3)の式3つ中における未知数は\(a_x,a_y,A,N\)の4個あるので、このままでは式の数が1つ足りない。そこで、図3のように台上の観測者から球の運動を眺めてみよう。動く台上から見ると、相対加速度が見える。1-30-1の通り「台から見た」の方で引き算して、球の相対加速度の\(x\)成分\(a’_x=a_x-A\)、\(y\)成分\(a’_y=a_y-0\)(台の加速度の\(y\)成分0を引くという意味)。ところでタクシーに乗っている人から見ると自分の足元は止まって見えるのと同様に、台上の人から見ると足元の台は止まって見える。こうして台上の観測者からは台があたかも固定台のように見え、球は斜面に沿って動いて見えるから、相対加速度の向きも斜面に沿って下向き。すると、\(a’_x>\)0に対して\(a’_y<\)0と逆符号であることに注意して、\(a’_y=-a’_x\tan\theta \)が成り立つことが分かる(\(a’_x\)と\(a’_y\)は逆符号だから\(a’_y=+a’_x\tan\theta \)とはならない)。よって
\(a_y=-(a_x-A)\tan\theta \) (4)
これで(1)から(4)まで式が4つ出揃ったことになり、あとは計算をすればよい。

とその前に、(4)のような加速度の条件式を「束縛条件」という。この用語のニュアンスは ―― 垂直抗力\(N\)が働く場合、球が斜面から離れずに運動しているからこそ\(N\)が働く。ということは、球は自由気ままに空中に飛んだり跳ねたりせず、斜面上に縛られている。その縛りのかけられ方(相対加速度が斜面に平行下向き)を表した式が(4)だから、「束縛」条件という。仮にこの問題が動く台ではなく、固定台の問題だったなら、斜面に垂直な方向の加速度\(a=\)0(斜面から離れずに運動していることを表す)を束縛条件という。
(1)から(4)の連立方程式の解き方としては、(1)(2)(3)の運動方程式を質量で割り算して\(a_x,a_y,A\)の式をつくり、それを(4)に代入すると\(N\)について解けて、再び(1)(2)(3)に戻してやれば\(a_x,a_y,A\)も求まる、とやるのが手早い。
(1)÷\(m\) \(\displaystyle a_x=\frac{\sin\theta}{m} N\) (1′)
(2)÷\(m\) \(\displaystyle a_y=\frac{\cos\theta}{m}N-g \; \) (2′)
(3)÷\(M\) \(\displaystyle A=-\frac{\sin\theta}{M} N \;\: \) (3′)
(4)に代入 \(\displaystyle \frac{\cos\theta}{m}N-g=-\left(\frac{\sin\theta}{m} N+\frac{\sin\theta}{M} N\right)\frac{\sin\theta}{\cos\theta} \)
両辺\(Mm\cos\theta\) 倍して
\(M\cos^2\theta\cdot N -Mm\cos\theta\cdot g=-M\sin^2\theta\cdot N -m\sin^2\theta\cdot N \)
\(N\)について整理
\((\,M(\cos^2\theta+\sin^2\theta)+m\sin^2\theta\,)N=Mm\cos\theta\cdot g \)
∴ \(N=\)\(\displaystyle \frac{Mm\cos\theta}{M+m\sin^2\theta} g \) [ 緑の下線は入試でよく聞かれる問題の答という意味 ] 予告済みの通り、\(N=mg\cos\theta \) にならなかった。
(1′)より \(\displaystyle a_x=\frac{\sin\theta}{m} \frac{Mm\cos\theta}{M+m\sin^2\theta} g= \)\(\displaystyle \frac{M\sin\theta\cos\theta}{M+m\sin^2\theta} g \)
(2′)より \(\displaystyle a_y=\frac{\cos\theta}{m} \frac{Mm\cos\theta}{M+m\sin^2\theta} g -g \)\(\displaystyle = \frac{M\cos^2\theta-\; (M+m\sin^2\theta)}{M+m\sin^2\theta} g \)
分子\(=-M(1-\cos^2\theta)-m\sin^2\theta=-M\sin^2\theta-m\sin^2\theta\)
\(=-(M+m)\sin^2\theta \) ∴ \(a_y=\)\(\displaystyle -\frac{(M+m)\sin^2\theta}{M+m\sin^2\theta} g \)
(3′)より \(\displaystyle A=-\frac{\sin\theta}{M} \frac{Mm\cos\theta}{M+m\sin^2\theta} g= \)\(\displaystyle -\frac{m\sin\theta\cos\theta}{M+m\sin^2\theta} g \)
ここまでの計算は実は入試で頻出なので、しっかり2度3度練習をしておこう。これらの答を元に、次の単元1-33-2でさらに考察を深めていくことにする。
→ 束縛条件(張力に伴う条件) は1-34-1へ


