2-06-2: 反射波の波の式

波の反射を波の式の観点で捉え直します。必要なら2-03-1: 波の式 を学習しておきましょう。

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

　1⃣　2-06-1で波の反射端では　反射波の変位＝(\( \pm 1\))×入射波の変位（自由端は(\(+1\))、固定端は(\(-1\))）となることを説明した。
　2⃣　一方2-01-1の通り、波動では「1点の振動が少しずつ遅れたタイミングで隣りの隣りの振動を引き起こしながら波形が平行移動していく」。
　1⃣ 2⃣ を組合わせると、波の反射に関して図１が書ける。まず図１の青い矢印は、ある1点\(x_0\)の振動が波形の平行移動とともに隣りへ隣りへと伝わっていく入射波の様子である。つまり波形(サインカーブ)の任意の高さ\(y\)(山の高さに限らない)に注目し、それが高さを保ちつつ移動していく様子だ。位置\(x_0\)での時刻は\(t_0\)であると書かれている。次に点線矢印は、壁(反射端)の右側にも媒質(例えばひも)があったならば引き続き振動が伝わっていく様子である。いま、
　入射波の(波の)式 \(\displaystyle y(x,t) =A\sin2\pi \left( \frac{t}{T}-\frac{x}{\lambda} \right) \)　　　　　　　(1)
が与えられたとしよう。これは2-03-1の通り、任意の位置\(x\)、任意の時刻\(t\)での波の変位(高さ)\(y\)を表す式。すると、点線矢印の例えば位置\(X\)、時刻\(t\)での高さ\(y\)は
　\(\displaystyle y(X,t) =A\sin2\pi \left( \frac{t}{T}-\frac{X}{\lambda} \right) \: \)　　　　　　　　　　　　　　 (2)
である。つまり、波の「式」という言い方はするが、それが表しているものは要は波の「高さ」だ。
　さて、図１の赤い矢印は、実際には壁の右側に媒質はないので波が左へと反射して伝わっていく様子である。1⃣より、壁の位置\(x=l\)で高さ(変位)が(\(-1\))倍になって反射するのが固定端、高さがそのまま(\(+1\))倍で反射するのが自由端。赤い矢印の任意の位置\(x\)、任意の時刻\(t\)での高さ\(y’\)が求まったならば、それが反射波の(波の)式\(y'(x,t)\)である。

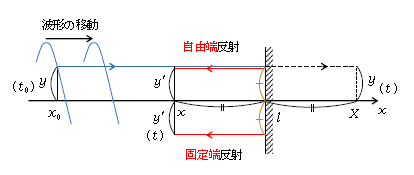
　ところで図１の位置\(X\)は、位置\(x\)の壁(\(x=l\))に関する対称点であることに注意しよう。なぜなら、\(x\)は壁から左へ、\(X\)は壁から右へ、同時刻\(t\)に波の伝わってくる点だからだ。すると中点公式より
　　\(\displaystyle \frac{x+X}{2}=l \)　　∴　\(X=2l-x \)　
　ここで図１より、赤い矢印の高さ\(y'(x,t)\)は点線矢印の高さ\(y(X,t)×(\pm 1)\)に等しいから
　反射波の式(高さ) \(y'(x,t)=(\pm 1)\)×入射波の式\(\displaystyle y(X,t)|_{X=2l-x} \:\, \)　 (3)
　　　(自由端は(\(+1\))、固定端は(\(-1\)))　　である。
　この式中の縦線 \(|\) の右下に\(X=2l-x\)のように添えると、「\(X\)に\(2l-x\)を代入しなさい」という意味になる。すなわち縦線は「ただし」のように読む。(2)を(3)に代入すると
　反射波の式 \(\displaystyle y'(x,t)=(\pm 1)×A\sin2\pi \left. \left( \frac{t}{T}-\frac{X}{\lambda} \right) \right |_{X=2l-x} \)
　　　　　　　　　　 \(\displaystyle =(\pm 1)×A\sin2\pi \left( \frac{t}{T}-\frac{2l-x}{\lambda} \right)\)
　　　　　　　　　　 \(\displaystyle =(\pm 1)×A\sin2\pi \left( \frac{t}{T}+\frac{x}{\lambda}-\frac{2l}{\lambda} \right) \: \)　　　(4)
のように求まる。2-03-1の通り、\(-x\)方向に進む反射波の式では\(\sin\)の中身の\(t\)と\(x\)が同符号で入っていることに注意しよう。

　さて、2-06-1で反射波形の描き方として、自由端なら「入射波形を壁越しに書き連ねたものをそのまま折り返す」、固定端なら「入射波形を壁越しに書き連ねたものを上下逆さまにしてから折り返す」と述べた。図１を見ればそれが正しかったことは明らかだ。なぜなら、(\(t\)を固定した上で)対称な位置\(x\)と\(X\)の\(y’=\pm y\)の関係が、いたる所の\(x\)について成り立っている。
　最後に ―― (1)のように入射波の式\(\)が与えられた前提で話を進めたが、問題で与えられていないなら自分で入射波の式をつくらねばならない。その方法は2-03-1で述べた通りである。