5-05-1: 球形容器の分子運動論 <例題>
5-04-1,5-04-2,5-04-3の立方体容器の分子運動論を、球形容器の場合に応用しましょう!
※ スマホで見る際は、画面を横長にして見ることをおすすめします。画面を縦長にして持つと、スマホしだいでは本文の右端がキレてしまうようです。
例題
半径\(r\)の球形の容器(中心O)に絶対温度\(T\)、分子の質量が\(m\)の単原子分子からなる理想気体が\(n\) mol入っている。分子は容器の壁と弾性衝突をし、分子どうしの衝突はないものとする。アボガドロ数を\(N_A\)、気体定数を\(R\)とする。
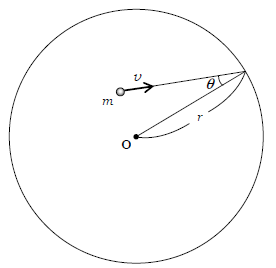
問1 図のように、入射角\(\theta\)で速さ\(v\)の分子が壁にぶつかり弾性衝突して跳ね返った。この分子の運動量の変化の大きさはいくらか。
問2 跳ね返ったこの分子が、次に壁にぶつかるまでに進む距離はどれほどか。
問3 この分子は単位時間あたりに何回容器の壁にぶつかるか。
問4 この分子が単位時間あたりに壁に与える力積の大きさの和はいくらか。
問5 この容器の中の分子は熱運動によりいろいろな速さと入射角で壁に衝突を繰り返している。\(n\) molの気体分子についての速度の2乗の平均\(\overline{v^2}\)を用いると、この気体の圧力はどのように表されるか。
問6 問4の結果と理想気体の状態方程式を用いると、分子1個あたりの平均の運動エネルギーはどのように表されるか。\(m,N_A,R,T\)の中から必要なものを用いて表せ。
問7 300Kのヘリウム気体中の分子運動の平均の速さ\(\sqrt{\overline{v^2}}\)は375Kのネオン気体中の分子運動の\(\sqrt{\overline{v^2}}\)の何倍か。有効数字2桁で答えよ。ただし、1molの質量はヘリウムが4.0\(\text{g}\)、ネオンが2.0×10\(\text{g}\)とする。
解答・解説
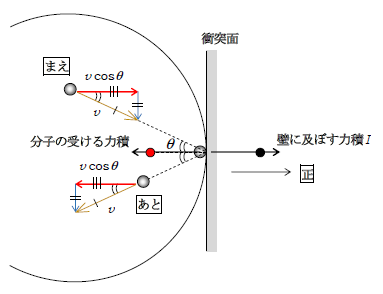
問1 球形容器のような曲面との衝突では、衝突面として、曲面の接平面を想定するとよい(図1)。5-04-1でやった通り、「固定面との弾性衝突では等角反射が起こる」。衝突面の法線方向に正の向きが図示してある。正方向について
分子の運動量変化(あとーまえ)\(=(-mv\cos\theta)-mv\cos\theta=-2mv\cos\theta\) (1)
その大きさ\(=\) 答 \(2mv\cos\theta\)
・ ここで、問3を見越して「1分子が1回の衝突で壁に及ぼす力積\(I\)」を求めておくと、
壁に及ぼす力積\(I\)\(=(-1)×\)(分子の受ける力積)\(=(-1)×\)(分子の運動量変化)
[ (1)を代入 ] \(=2mv\cos\theta\,\) (2)
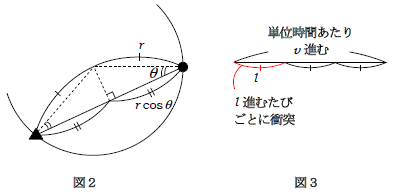
問2 求める距離\(l\)は、図2の●印と▲印を結ぶ距離である。
よって \(l=\) 答 \(2r\cos\theta\)
問3 単位時間あたりの衝突回数\(N_1\)を求めるには、5-04-2の②でやった通り、速さ\(v\)を距離\(l\)で割ればよい(図3を参照)。
\(\displaystyle N_1=\frac{v}{l}=\) [ 問2の\(l\)を代入 ] 答 \(\displaystyle \frac{v}{2r\cos\theta}\)
問4 5-04-2の③の通り、単位時間あたりに壁に及ぼす力積
\(=\)1分子が1回の衝突で壁に及ぼす力積\(I\)×単位時間あたりの衝突回数\(N_1\)
[ (2)を代入 ] \(\displaystyle =2mv\cos\theta×\frac{v}{2r\cos\theta}\) 答 \(\displaystyle \frac{mv^2}{r}\)
問5 問4で求めた「単位時間あたりに壁に及ぼす力積」の単位は、力積の単位 [N\(\cdot \)s]を単位時間あたりになおすために[s]で割った[N]、すなわち力の単位に等しい。つまり「単位時間あたりに壁に及ぼす力積」は「1分子が壁に及ぼす力(を時間的に一定とみなしたもの)\(f_1\)」である(詳しくは5-04-2の③を参照のこと):
\(\displaystyle f_1=\frac{mv^2}{r}\)
いま、アボガドロ数\(N_A\)とは1molあたりの分子数だから、全分子数は\(nN_A\)。ゆえに「1分子が壁に及ぼす力\(f_1\)」を分子数\(nN_A\)個分合計すれば、「分子全体が壁に及ぼす力\(F\)」が得られる。その合計\(F\)を得るには、分子\(nN_A\)個分にわたる\(f_1\)の平均値\(\displaystyle f=\frac{m\overline{v}^2}{r}\) [ \(f_1\)の式の中の\(v\)を「平均」を意味する\(\overline{v}\)で置き換えてある ] を、分子数\(nN_A\)倍すればよい。
\(\displaystyle F= \frac{m\overline{v}^2}{r}×nN_A=\frac{nN_Am\overline{v}^2}{r}\)
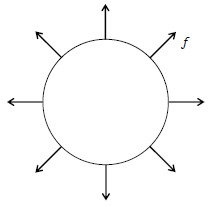
なお、球形容器を扱っているので、この\(F\)は様々な方向の\(f\)を(\(x,y\)成分に分解することなく)単純に足し上げたもののことである(図4)。
求める圧力\(P\)とは単位面積当たりの力だから、力\(F\)を壁の面積(球の表面積\(4\pi r^2\))で割って
\(\displaystyle P= \frac{F}{4\pi r^2}=\frac{nN_Am\overline{v}^2}{r}\frac{1}{4\pi r^2}=\) 答 \(\displaystyle \frac{nN_Am\overline{v}^2}{4\pi r^3}\)
問6 まず問5の答を\(\displaystyle P=\frac{nN_Am\overline{v}^2}{3×\frac{4}{3}\pi r^3}\) のように変形すれば、球形容器の体積\(\displaystyle V=\frac{4}{3}\pi r^3\)だから、
\(\displaystyle P=\frac{nN_Am\overline{v}^2}{3V}\) これは5-04-03で導いた立方体容器の圧力公式と一致していることが分かる。分母の\(3V\)を払ってさらに2で割ると
\(\displaystyle \frac{3}{2}PV=nN_A\frac{m}{2}\overline{v}^2\) 左辺を状態方程式で書き換えると、
\(\displaystyle \frac{3}{2}nRT=nN_A\frac{m}{2}\overline{v}^2\) よって1分子の平均運動エネルギーは
\(\displaystyle \frac{m}{2}\overline{v}^2=\) 答 \(\displaystyle \frac{3}{2}\frac{R}{N_A}T\)
・ 5-04-03(II)の通り、ボルツマン定数\(\displaystyle k=\frac{R}{N_A}\)であるから、
気体分子の平均運動エネルギー \(\displaystyle \frac{m}{2}\overline{v}^2=\frac{3}{2}kT\) これも立方体容器の公式と一致している。
問7 問6の答を\(\displaystyle \frac{N_Am}{2}\overline{v}^2=\frac{3}{2}RT\) と変形してみると、左辺の分子の\(N_Am\)は、問題文中の「1molの質量」として与えられている量(4.0\(\text{g}\)、2.0×10\(\text{g}\))のことである。この式をヘリウムについてはHeの添え字を付けて
\(\displaystyle \frac{N_Am_\text{He}}{2}{\overline{v_\text{He}}}^2=\frac{3}{2}RT_\text{He}\) のように表し、ネオンについてはNeの添え字で
\(\displaystyle \frac{N_Am_\text{Ne}}{2}{\overline{v_\text{Ne}}}^2=\frac{3}{2}RT_\text{Ne}\) のように表す。2式を割り算すれば
\(\displaystyle \frac{m_\text{He}}{m_\text{Ne}}\frac{{\overline{v_\text{He}}}^2}{{\overline{v_\text{Ne}}}^2}=\frac{T_\text{He}}{T_\text{Ne}}\) (3)
∴ \(\displaystyle \frac{{\overline{v_\text{He}}}^2}{{\overline{v_\text{Ne}}}^2}=\frac{m_\text{Ne}}{m_\text{He}}\frac{T_\text{He}}{T_\text{Ne}}=\frac{2.0×10\,\text{g}}{4.0\,\text{g}}\frac{300\,\text{K}}{375\,\text{K}}=4.0\)
よって、求める\(\displaystyle \frac{\sqrt{{\overline{v_\text{He}}}^2}}{\sqrt{{\overline{v_\text{Ne}}}^2}}=\) 答 \(2.0\)
・ このように2式を割り算すると、余計な定数\(N_A\)や\(R\)が消去できて、見やすい式(3)が得られる。役に立つ計算方法として参考にしてほしい。


