6-06-3: ボーアモデル #その３

いよいよボーアモデルのクライマックスです！　→　＜#その1＞は6-06-1、＜#その2＞は6-06-2へ　　　　　　　　　　　　　　　

　6-06-1の(☆)定常状態の仮説および(II)量子条件は、原子の安定性を保証する、つまり原子が光を放出しないための仮説であった。しかし、このままでは光を放出する現象としての水素原子のスペクトル(6-06-1)を、当然説明することができない。そこで次の仮説に移ろう。

(III) 振動数条件の仮説　

　この仮説によれば、電子がエネルギー準位を変える(「遷移」すると言う)とき、ちょうどそのエネルギー差分のエネルギーを持った光子を1個放出または吸収し、そのとき振動数条件：
　\(\displaystyle h\nu=h\frac{c}{\lambda}=E_n-E_l \)　（\(n,l\)は\(n>l\)を満たす整数）　　(6)　
（図１）が成り立つ。

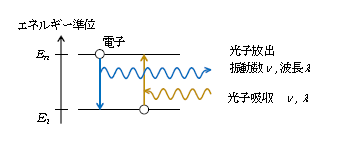
　図１で1光子が放出される場合のエネルギー保存則は、初め電子が\(E_n\)の状態にあり、終りには\(E_l\)の状態で光子が新たに生成しているから　
　　\(E_n=E_l+h\nu \)。これは(6)と同値である。
　また、1光子が吸収される場合は、初め電子が\(E_l\)で光子が存在し、終りは\(E_n\)で光子が消滅しているから　
　　\(E_l+h\nu=E_n \)。これも(6)と同値。つまり、(6)は電子の遷移に伴って光子が生成・消滅すると仮定したときのエネルギー保存則である。

・　水素原子のスペクトルの説明
　唐突の感は否めないのだが、\(\displaystyle R=\frac{2\pi^2 k^2 e^4 m}{h^3 c} \)とおく。　　　(7)
　すると、6-06-2の式(5)　\(\displaystyle E_n=-\frac{2\pi^2 k^2 e^4 m}{h^2} \frac{1}{n^2} \)　は
　　\(\displaystyle E_n=-hcR \frac{1}{n^2} \)　と書き換えられる。
　これを(6)に代入すると　\(\displaystyle h\frac{c}{\lambda}=-hcR \frac{1}{n^2} +hcR \frac{1}{l^2} \)
　両辺\(hc\)で約分して　\(\displaystyle \frac{1}{\lambda}=R\left( \frac{1}{l^2} – \frac{1}{n^2} \right) \; \)　　　　　　　　　(8)
　これは式の形としては、6-06-1で述べたリュードベリの公式と一致する。のみならず、(7)の右辺の量に実験データを代入してみると\(R=1.1×10^7 \)1/m となって、当時実験的に定まっていたリュードベリ定数\(R\)と(誤差の範囲内で)一致する。

・　ボーアモデルを歴史的に振り返る
　ボーアが彼の理論を発表した当時の物理学会の受け止めは、否定派・肯定派相混じっていたようである。
　否定派からすると、ボーアモデルはとにかく欠陥だらけの理論だったということに尽きる。6-06-1で触れた通り、ボーアは量子条件の意味を事実上説明していない。また、量子条件の仮説で原子は発光せずに安定だと主張する一方で、振動数条件の仮説では原子は発光すると述べる。しかも、いつ、どのようなメカニズムで発光するのか、電子がある軌道から別の軌道に移る遷移中の様子はどのようなものかなどには全く触れていない。　　(＊)
　一方、肯定派からすると、 それにしても数式(7)と、実験的に得られたリュードベリ定数との一致は、とてもまぐれ当たりとは考えられない。ボーアの理論には控えめに言っても部分的な真実があると見るべきで、不備のあるように見える理論の中にむしろ当時の物理学が見落としていた真理が隠されているのかもしれないではないか。
　さて、現代人の我々は、ボーアモデルは原子番号１という単純な原子構造を持つ水素には当てはまるが、原子番号２以上の例えばヘリウムについては適用できず破綻するということを知っている。ヘリウム以上の原子番号の原子については、全く成り立たない理論なのだ。
　結局のところ、現代人の後知恵として見ると、ボーアモデルの正否に関しては以下のようにまとめることができる。
　(I)　古典力学の仮説は、表面上その数式自体は正しくても、実はその数式にハイゼンベルクの行列力学に基づくより高度な数学的演算・物理的解釈(大学の内容)を適用しなければならなかったのである。
　(II) 量子条件の仮説は、水素が単純な原子構造を持っていたからこそ上手く行っただけの話で、一般の原子(水素を含む！)に対しては、シュレーディンガーの波動力学に基づく修正・更新が必要となる。6-06-2で量子条件の意味をドブロイ波長に関連付けて説明した際「（のではないだろうか）」という回りくどい言い回しをしたのは、現代の量子力学からしてどのみち正確でない説明をしたからである。
　(III) 振動数条件の仮説は、驚くべきことに、現代物理学からしても「全く」正しい。何と(＊)の緑の下線部を加味したとしても全く正しいのである（これについては、少なくとも量子力学の「不確定性原理」を大学で学ぶ必要がある）。
　してみると、ボーアモデルは現代物理学における金字塔「量子力学」（「相対性理論」とともに実験的な反例がただの１つも見つかっていない理論！）へと至る過渡期の理論であり、ボーアの卓越した洞察力なくしてはあり得なかった、重要なバトンリレーの中継点なのである。

・　水素原子のスペクトルについての補足（図２）
　(8)で\(l=1\)とすると　\(\displaystyle \frac{1}{\lambda_n}=R\left( 1 – \frac{1}{n^2} \right) \)　（\(n\)≧2)
　　この\(\lambda_2,\lambda_3,\cdots \)をライマン系列といい、紫外線に相当する。
　\(l=2\)とすると　\(\displaystyle \frac{1}{\lambda’_n}=R\left( \frac{1}{4} – \frac{1}{n^2} \right) \)　（\(n\)≧3)
　　\(\lambda’_3,\lambda’_4,\cdots \)をバルマー系列といい、可視光線に相当する。目に見える光だけに、歴史上最も速く発見された系列である(1885年)。
　\(l=3\)とすると　\(\displaystyle \frac{1}{\lambda’’_n}=R\left( \frac{1}{9} – \frac{1}{n^2} \right) \)　（\(n\)≧4)
　　\(\lambda’’_4,\lambda’’_5,\cdots \)をパッシェン系列といい、赤外線に相当する。
　他にも\(l=4,5,\cdots \)と固有の系列名は続くが、大学入試では\(l=3\)までを押さえれば十分である。

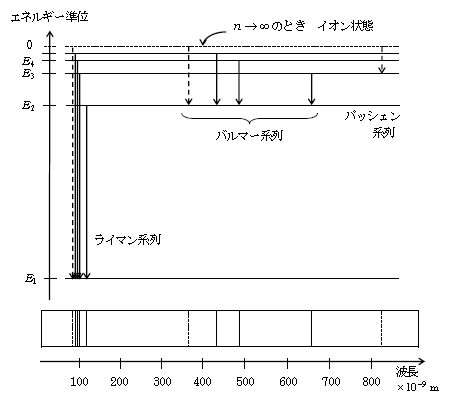
　図２のそれぞれの系列において、縦軸の\(E_n\)の\(n\)が大きくなるほど、横軸の波長\(\lambda\)が小さくなっている。その理由は、(8)式　\(\displaystyle \frac{1}{\lambda}=R\left( \frac{1}{l^2} – \frac{1}{n^2} \right) \)　で\(n\)が大きくなるほど\(\displaystyle \frac{1}{n^2} \)が小さくなり、\(\displaystyle \frac{1}{n^2} \)に（\(-\)）が付いているということは右辺が大きくなり、すなわち左辺が大きくなり、\(\lambda\)が小さくなるからである。これは\(n\)が大きくなるほど、(6)より光子の\(\displaystyle h\nu=h\frac{c}{\lambda} \)が大きくなることに対応している。